Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo

Bài tập 2 trang 97 SGK Toán 9 tập 1 thuộc chương trình Toán 9 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về cách xác định hệ số góc, đường thẳng song song và các ứng dụng của hàm số bậc nhất.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung (oversetfrown{BD};oversetfrown{BE};oversetfrown{EC}).

Đề bài

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo 1

- Đọc dữ kiện đề bài để vẽ hình.

- Chứng minh hai tam giác BOD và EOC là tam giác đều, tính \(\widehat {DOE}\) rồi so sánh các góc suy ra \(\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}\)

Lời giải chi tiết

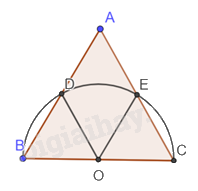
Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo 2

Gọi O là tâm đường tròn đường kính BC.

Ta có OB = OD (= R)

Vậy tam giác BOD cân tại O

Mà \(\widehat {DBO}\)= 60^o nên tam giác BOD đều

Suy ra \(\widehat {DOB}\)= 60^o

OE = DC (= R)

Vậy tam giác EOC cân tại O

Mà \(\widehat {ECO}\)= 60^o nên tam giác EOC đều

Suy ra \(\widehat {EOC}\)= 60^o

Ta có \(\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}\)

Suy ra 60^o+ \(\widehat {DOE} + {60^o} = {180^o}\) nên \(\widehat {DOE} = {60^o}\)

Vì \(\widehat {BOD} = \widehat {DOE} = \widehat {EOC} = {60^o}\) nên sđ\(\overset\frown{BD}\) = sđ\(\overset\frown{BE}\) = sđ\(\overset\frown{EC}={{60}^{o}}\)

Vậy \(\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}\)

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 9 trên nền tảng tài liệu toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết

Bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:

Hàm số bậc nhất: Dạng y = ax + b, trong đó a là hệ số góc, b là tung độ gốc.
Hệ số góc: Xác định độ dốc của đường thẳng. Nếu a > 0, hàm số đồng biến; nếu a < 0, hàm số nghịch biến.
Đường thẳng song song: Hai đường thẳng song song khi và chỉ khi chúng có cùng hệ số góc và khác tung độ gốc.

Phân tích bài toán

Trước khi đi vào giải bài tập, chúng ta cần phân tích đề bài để xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp các thông tin về một tình huống thực tế, ví dụ như quãng đường đi được của một vật, sự thay đổi nhiệt độ theo thời gian, hoặc mối quan hệ giữa số lượng sản phẩm và doanh thu. Dựa vào các thông tin này, chúng ta sẽ xây dựng được phương trình hàm số bậc nhất mô tả mối quan hệ đó.

Phương pháp giải

Để giải bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo, chúng ta có thể áp dụng các bước sau:

Xác định các điểm thuộc đường thẳng: Dựa vào thông tin đề bài, xác định ít nhất hai điểm thuộc đường thẳng cần tìm.
Tìm hệ số góc: Sử dụng công thức tính hệ số góc a = (y2 - y1) / (x2 - x1) với (x1, y1) và (x2, y2) là hai điểm đã xác định.
Tìm tung độ gốc: Thay một trong các điểm đã xác định và hệ số góc vừa tìm được vào phương trình y = ax + b để tìm b.
Viết phương trình hàm số: Thay hệ số góc a và tung độ gốc b vào phương trình y = ax + b để có phương trình hàm số cần tìm.
Kiểm tra lại kết quả: Thay các điểm đã cho vào phương trình hàm số vừa tìm được để kiểm tra xem chúng có thỏa mãn phương trình hay không.

Ví dụ minh họa

Giả sử đề bài cho biết một vật chuyển động đều với vận tốc 2m/s và ban đầu cách điểm gốc 5m. Hãy tìm phương trình hàm số biểu diễn quãng đường đi được của vật theo thời gian.

Giải:

Xác định các điểm: Tại thời điểm t = 0, quãng đường đi được là s = 5m. Tại thời điểm t = 1, quãng đường đi được là s = 7m.
Tìm hệ số góc: a = (7 - 5) / (1 - 0) = 2.
Tìm tung độ gốc: Thay điểm (0, 5) vào phương trình y = 2x + b, ta có 5 = 2 * 0 + b, suy ra b = 5.
Viết phương trình hàm số: s = 2t + 5.

Luyện tập thêm

Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập đa dạng với lời giải chi tiết, giúp các em tự tin hơn trong quá trình học tập.

Kết luận

Bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bằng cách nắm vững kiến thức và áp dụng phương pháp giải đúng đắn, các em học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự khác.

Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài tập 2 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.