Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 77, 78 SGK Toán 9 tập 2 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học sinh học tập hiệu quả.
Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là H) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông H trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của H tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông H quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của H trùng lại với đỉnh A (Hình 5d).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 78 SGK Toán 9 Chân trời sáng tạo
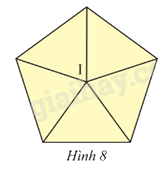
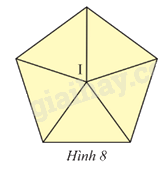
Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).
Phương pháp giải:
Dựa vào phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M’ thuộc đường tròn (O;OM) sao cho khi tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MM’ có số đo \({\alpha ^o}\). Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O. Phép quay \({0^o}\) hay \({360^o}\) giữ nguyên mọi điểm.
Lời giải chi tiết:
Đỉnh I của ngũ giác đều chia đường tròn (I) thành 5 cung bằng nhau, mỗi cung đo có số đo 72o. Từ đó, các phép quay biến ngũ giác đều thành chính nó là các phép quay 72o, 144o, 216o, 288o hoặc 360o tâm I cùng chiều kim đồng hồ hay ngược chiều kim đồng hồ.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 78 SGK Toán 9 Chân trời sáng tạo
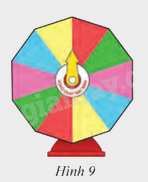
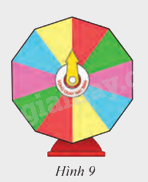
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó.
Phương pháp giải:
Dựa vào phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M’ thuộc đường tròn (O;OM) sao cho khi tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MM’ có số đo \({\alpha ^o}\). Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O. Phép quay \({0^o}\) hay \({360^o}\) giữ nguyên mọi điểm.
Lời giải chi tiết:
10 đỉnh của đa giác đều, 10 cạnh chia đường tròn thành 10 cung bằng nhau mỗi cung có số đo 36o. Từ đó, các phép quay biến đa giác đều 10 cạnh thành chính nó là các phép quay 36o, 72o, 108o, 144o, 180o, 216o, 252o, 288o, 324o, 360o; tâm đường tròn cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 77 SGK Toán 9 Chân trời sáng tạo
Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là H) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông H trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của H tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông H quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của H trùng lại với đỉnh A (Hình 5d).
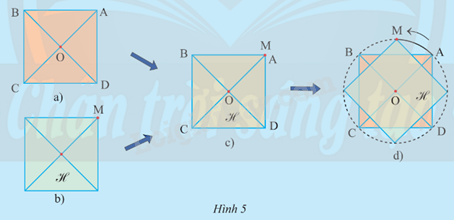
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng bao nhiêu?
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD bao nhiêu lần (không tính vị trí ban đầu trước khi quay)? Ứng với mỗi lần đó, điểm M vạch nên cung có số đo bao nhiêu?
Phương pháp giải:
Nhìn hình tính vòng quay rồi nhận xét.
Lời giải chi tiết:
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng 90o.
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD 4 lần (không tính vị trí ban đầu trước khi quay).
- Lần 1, điểm M vạch lên cung số đo 90o.
- Lần 2, điểm M vạch lên cung số đo 180o.
- Lần 3, điểm M vạch lên cung số đo 270o.
- Lần 4, điểm M vạch lên cung số đo 360o.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 77 SGK Toán 9 Chân trời sáng tạo
Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là H) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông H trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của H tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông H quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của H trùng lại với đỉnh A (Hình 5d).
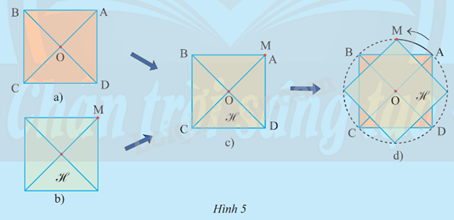
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng bao nhiêu?
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD bao nhiêu lần (không tính vị trí ban đầu trước khi quay)? Ứng với mỗi lần đó, điểm M vạch nên cung có số đo bao nhiêu?
Phương pháp giải:
Nhìn hình tính vòng quay rồi nhận xét.
Lời giải chi tiết:
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng 90o.
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD 4 lần (không tính vị trí ban đầu trước khi quay).
- Lần 1, điểm M vạch lên cung số đo 90o.
- Lần 2, điểm M vạch lên cung số đo 180o.
- Lần 3, điểm M vạch lên cung số đo 270o.
- Lần 4, điểm M vạch lên cung số đo 360o.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 78 SGK Toán 9 Chân trời sáng tạo
Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).
Phương pháp giải:
Dựa vào phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M’ thuộc đường tròn (O;OM) sao cho khi tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MM’ có số đo \({\alpha ^o}\). Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O. Phép quay \({0^o}\) hay \({360^o}\) giữ nguyên mọi điểm.
Lời giải chi tiết:
Đỉnh I của ngũ giác đều chia đường tròn (I) thành 5 cung bằng nhau, mỗi cung đo có số đo 72o. Từ đó, các phép quay biến ngũ giác đều thành chính nó là các phép quay 72o, 144o, 216o, 288o hoặc 360o tâm I cùng chiều kim đồng hồ hay ngược chiều kim đồng hồ.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 78 SGK Toán 9 Chân trời sáng tạo
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó.
Phương pháp giải:
Dựa vào phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M’ thuộc đường tròn (O;OM) sao cho khi tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MM’ có số đo \({\alpha ^o}\). Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O. Phép quay \({0^o}\) hay \({360^o}\) giữ nguyên mọi điểm.
Lời giải chi tiết:
10 đỉnh của đa giác đều, 10 cạnh chia đường tròn thành 10 cung bằng nhau mỗi cung có số đo 36o. Từ đó, các phép quay biến đa giác đều 10 cạnh thành chính nó là các phép quay 36o, 72o, 108o, 144o, 180o, 216o, 252o, 288o, 324o, 360o; tâm đường tròn cùng chiều kim đồng hồ hoặc ngược chiều kim đồng hồ.
Mục 2 của chương trình Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Mục 2 trang 77, 78 SGK Toán 9 tập 2 - Chân trời sáng tạo bao gồm các bài tập sau:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy xác định các yếu tố của hàm số, tìm đỉnh của parabol và vẽ đồ thị hàm số.
Lời giải:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Ví dụ: Giải phương trình x2 - 5x + 6 = 0.
Lời giải:
Phương trình có thể được phân tích thành nhân tử như sau: (x - 2)(x - 3) = 0. Vậy phương trình có hai nghiệm là x = 2 và x = 3.
Để giải bài tập này, học sinh cần:
Hy vọng rằng bài giải chi tiết mục 2 trang 77, 78 SGK Toán 9 tập 2 - Chân trời sáng tạo trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải quyết các bài toán liên quan đến hàm số bậc hai. Chúc các em học tập tốt!