Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 49, 50 SGK Toán 9 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 tập trung vào các kiến thức về hàm số bậc nhất, bao gồm việc xác định hệ số góc, vẽ đồ thị và ứng dụng vào giải quyết các bài toán thực tế.
Thực hiện các phép tính có trên bảng trong Hình 2. b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 6 trang 50 SGK Toán 9 Chân trời sáng tạo
Tính
a) \(\sqrt {\frac{9}{{25}}} \)
b) \(\sqrt {1\frac{9}{{16}}} \)
c) \(\sqrt {150} :\sqrt 6 \)
d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} \)
Phương pháp giải:
Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:
\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)
Lời giải chi tiết:
a) \(\sqrt {\frac{9}{{25}}} = \frac{{\sqrt 9 }}{{\sqrt {25} }} = \frac{3}{5}\)
b) \(\sqrt {1\frac{9}{{16}}} = \sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4}\)
c) \(\sqrt {150} :\sqrt 6 = \sqrt {\frac{{150}}{6}} = \sqrt {25} = 5\)
d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} = \sqrt {\frac{3}{5}:\frac{5}{{12}}} = \sqrt {\frac{3}{5}.\frac{{12}}{5}} = \sqrt {\frac{{36}}{{25}}} = \frac{{\sqrt {36} }}{{\sqrt {25} }} = \frac{6}{5}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 7 trang 50 SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }}\)
b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} \) với \(a \ge 0;b \ne 0\)
c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }}\) với a > 1
Phương pháp giải:
Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:
\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)
Lời giải chi tiết:
a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }} = \sqrt {\frac{{555}}{{111}}} = \sqrt 5 \)
b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} = \frac{{\sqrt {{a^2}} }}{{\sqrt {4{b^4}} }} = \frac{a}{{2{b^2}}}\)
c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }} = \sqrt {\frac{{2{a^2}{{(1 - a)}^2}}}{{50}}} = \sqrt {\frac{{{a^2}{{(1 - a)}^2}}}{{25}}} = \frac{{\sqrt {{a^2}{{(1 - a)}^2}} }}{{\sqrt {25} }} = \frac{{a(a-1)}}{5}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 50 SGK Toán 9 Chân trời sáng tạo
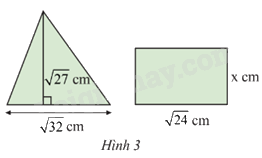
Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.
Phương pháp giải:
Dựa vào công thức diện tích tam giác S = \(\frac{1}{2}a.h\) (h: chiều cao,a: độ dài đáy) và diện tích hình chữ nhật S = a.b (a:chiều dài; b: chiều rộng).
Lời giải chi tiết:
Diện tích tam giác là: \(\frac{1}{2}.\sqrt {27} .\sqrt {32} = \frac{1}{2}.\sqrt {3.9} .\sqrt {16.2} = \frac{1}{2}.3\sqrt 3 .4\sqrt 2 = 6\sqrt 6 \) cm2
Suy ra diện tích hình chữ nhật là \(6\sqrt 6 \) cm2
Vậy x = \(\frac{{6\sqrt 6 }}{{\sqrt {24} }} = \frac{{6\sqrt 6 }}{{2\sqrt 6 }} = 3\)cm.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 49SGK Toán 9 Chân trời sáng tạo
a) Thực hiện các phép tính có trên bảng trong Hình 2.

b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?
Phương pháp giải:
Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}} = a\). ( a > 0)
Lời giải chi tiết:
a)
(1) \(\sqrt {\frac{4}{9}} = \sqrt {{{\left( {\frac{2}{3}} \right)}^2}} = \frac{2}{3}\)
(2) \(\frac{{\sqrt 4 }}{{\sqrt 9 }} = \frac{{\sqrt {{2^2}} }}{{\sqrt {{3^2}} }} = \frac{2}{3}\)
(3) \(\sqrt {\frac{{16}}{{25}}} = \sqrt {{{\left( {\frac{4}{5}} \right)}^2}} = \frac{4}{5}\)
(4) \(\frac{{\sqrt {16} }}{{\sqrt {25} }} = \frac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \frac{4}{5}\)
b) Căn bậc hai của thương hai số dương bằng thương của căn bậc hai hai số dương.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 49SGK Toán 9 Chân trời sáng tạo
a) Thực hiện các phép tính có trên bảng trong Hình 2.

b) Từ đó, có nhận xét gì về căn bậc hai của thương hai số dương?
Phương pháp giải:
Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}} = a\). ( a > 0)
Lời giải chi tiết:
a)
(1) \(\sqrt {\frac{4}{9}} = \sqrt {{{\left( {\frac{2}{3}} \right)}^2}} = \frac{2}{3}\)
(2) \(\frac{{\sqrt 4 }}{{\sqrt 9 }} = \frac{{\sqrt {{2^2}} }}{{\sqrt {{3^2}} }} = \frac{2}{3}\)
(3) \(\sqrt {\frac{{16}}{{25}}} = \sqrt {{{\left( {\frac{4}{5}} \right)}^2}} = \frac{4}{5}\)
(4) \(\frac{{\sqrt {16} }}{{\sqrt {25} }} = \frac{{\sqrt {{4^2}} }}{{\sqrt {{5^2}} }} = \frac{4}{5}\)
b) Căn bậc hai của thương hai số dương bằng thương của căn bậc hai hai số dương.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 6 trang 50 SGK Toán 9 Chân trời sáng tạo
Tính
a) \(\sqrt {\frac{9}{{25}}} \)
b) \(\sqrt {1\frac{9}{{16}}} \)
c) \(\sqrt {150} :\sqrt 6 \)
d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} \)
Phương pháp giải:
Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:
\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)
Lời giải chi tiết:
a) \(\sqrt {\frac{9}{{25}}} = \frac{{\sqrt 9 }}{{\sqrt {25} }} = \frac{3}{5}\)
b) \(\sqrt {1\frac{9}{{16}}} = \sqrt {\frac{{25}}{{16}}} = \frac{{\sqrt {25} }}{{\sqrt {16} }} = \frac{5}{4}\)
c) \(\sqrt {150} :\sqrt 6 = \sqrt {\frac{{150}}{6}} = \sqrt {25} = 5\)
d) \(\sqrt {\frac{3}{5}} :\sqrt {\frac{5}{{12}}} = \sqrt {\frac{3}{5}:\frac{5}{{12}}} = \sqrt {\frac{3}{5}.\frac{{12}}{5}} = \sqrt {\frac{{36}}{{25}}} = \frac{{\sqrt {36} }}{{\sqrt {25} }} = \frac{6}{5}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 7 trang 50 SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }}\)
b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} \) với \(a \ge 0;b \ne 0\)
c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }}\) với a > 1
Phương pháp giải:
Dựa vào tính chất: Với số thực a không âm và số thực b dương, ta có:
\(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\)
Lời giải chi tiết:
a) \(\frac{{\sqrt {555} }}{{\sqrt {111} }} = \sqrt {\frac{{555}}{{111}}} = \sqrt 5 \)
b) \(\sqrt {\frac{{{a^2}}}{{4{b^4}}}} = \frac{{\sqrt {{a^2}} }}{{\sqrt {4{b^4}} }} = \frac{a}{{2{b^2}}}\)
c) \(\frac{{\sqrt {2{a^2}{{(1 - a)}^2}} }}{{\sqrt {50} }} = \sqrt {\frac{{2{a^2}{{(1 - a)}^2}}}{{50}}} = \sqrt {\frac{{{a^2}{{(1 - a)}^2}}}{{25}}} = \frac{{\sqrt {{a^2}{{(1 - a)}^2}} }}{{\sqrt {25} }} = \frac{{a(a-1)}}{5}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 50 SGK Toán 9 Chân trời sáng tạo
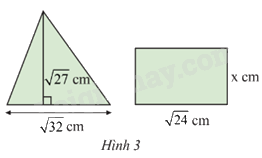
Biết rằng hình tam giác và hình chữ nhật ở Hình 3 có diện tích bằng nhau. Tính chiều rộng x của hình chữ nhật.
Phương pháp giải:
Dựa vào công thức diện tích tam giác S = \(\frac{1}{2}a.h\) (h: chiều cao,a: độ dài đáy) và diện tích hình chữ nhật S = a.b (a:chiều dài; b: chiều rộng).
Lời giải chi tiết:
Diện tích tam giác là: \(\frac{1}{2}.\sqrt {27} .\sqrt {32} = \frac{1}{2}.\sqrt {3.9} .\sqrt {16.2} = \frac{1}{2}.3\sqrt 3 .4\sqrt 2 = 6\sqrt 6 \) cm2
Suy ra diện tích hình chữ nhật là \(6\sqrt 6 \) cm2
Vậy x = \(\frac{{6\sqrt 6 }}{{\sqrt {24} }} = \frac{{6\sqrt 6 }}{{2\sqrt 6 }} = 3\)cm.
Mục 3 trong SGK Toán 9 tập 1 chương trình Chân trời sáng tạo tập trung vào việc nghiên cứu sâu hơn về hàm số bậc nhất. Các em học sinh sẽ được làm quen với các khái niệm như hệ số góc, đường thẳng song song và vuông góc, cũng như cách ứng dụng hàm số bậc nhất để giải quyết các bài toán thực tế.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a khác 0. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Để xác định hàm số bậc nhất, các em có thể sử dụng các thông tin sau:
Bài 1: Xác định hàm số bậc nhất có đồ thị đi qua hai điểm A(1; 2) và B(-1; 0).
Lời giải:
Thay tọa độ điểm A vào phương trình y = ax + b, ta có: 2 = a(1) + b => a + b = 2 (1)
Thay tọa độ điểm B vào phương trình y = ax + b, ta có: 0 = a(-1) + b => -a + b = 0 (2)
Giải hệ phương trình (1) và (2), ta được: a = 1 và b = 1.
Vậy hàm số bậc nhất cần tìm là: y = x + 1
Bài 2: Vẽ đồ thị hàm số y = 2x - 1.
Lời giải:
Xác định hai điểm thuộc đồ thị hàm số. Ví dụ:
Vẽ đường thẳng đi qua hai điểm A và B trên mặt phẳng tọa độ. Đó chính là đồ thị của hàm số y = 2x - 1.
Hàm số bậc nhất được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, ví dụ:
Để nắm vững kiến thức về hàm số bậc nhất, các em nên luyện tập thêm các bài tập trong SGK và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu rõ bản chất của các khái niệm và phương pháp giải bài tập.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn khi giải các bài tập về hàm số bậc nhất trong chương trình Toán 9 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!