Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 69 và 70 sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
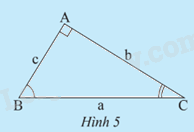
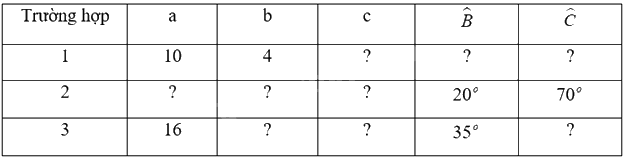
Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 70SGK Toán 9 Chân trời sáng tạo
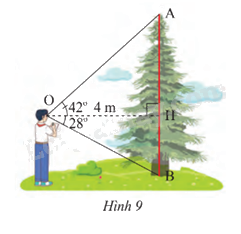
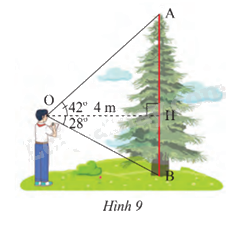
Trong Hình 9, cho OH = 4 m, \(\widehat {AOH} = {42^o},\widehat {HOB} = {28^o}\). Tính chiều cao AB của cây.
Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
Xét tam giác OHA vuông tại H, ta có
AH = tan 42\(^o\). OH = tan 42\(^o\). 4 \( \approx \) 3,6 (m)
Xét tam giác OHB vuông tại H, ta có
HB = tan 28\(^o\). OH = tan 28\(^o\). 4 \( \approx \) 2,1 (m)
Vậy chiều cao AB của cây là: AH + HB = 3,6 + 2,1 = 5,7 (m)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 69 SGK Toán 9 Chân trời sáng tạo
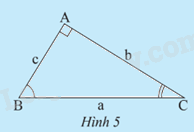
Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính.
Phương pháp giải:
- Áp dụng định lý Pythagore trong tam giác vuông
- Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang, kí hiệu cot.
Lời giải chi tiết:
Ta có thể tính được tất cả các cạnh và các góc của tam giác trong:
+ Trường hợp 1 vì chỉ cần biết hai cạnh của tam giác vuông ta sẽ tìm được cạnh còn lại và các góc từ tỉ số lượng giác.
+ Trường hợp 3 vì chỉ cần biết một cạnh và 1 góc của tam giác vuông ta sẽ tìm được cạnh còn lại và các góc từ tỉ số lượng giác
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 69 SGK Toán 9 Chân trời sáng tạo
Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính.
Phương pháp giải:
- Áp dụng định lý Pythagore trong tam giác vuông
- Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang, kí hiệu cot.
Lời giải chi tiết:
Ta có thể tính được tất cả các cạnh và các góc của tam giác trong:
+ Trường hợp 1 vì chỉ cần biết hai cạnh của tam giác vuông ta sẽ tìm được cạnh còn lại và các góc từ tỉ số lượng giác.
+ Trường hợp 3 vì chỉ cần biết một cạnh và 1 góc của tam giác vuông ta sẽ tìm được cạnh còn lại và các góc từ tỉ số lượng giác
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 70SGK Toán 9 Chân trời sáng tạo
Trong Hình 9, cho OH = 4 m, \(\widehat {AOH} = {42^o},\widehat {HOB} = {28^o}\). Tính chiều cao AB của cây.
Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
Xét tam giác OHA vuông tại H, ta có
AH = tan 42\(^o\). OH = tan 42\(^o\). 4 \( \approx \) 3,6 (m)
Xét tam giác OHB vuông tại H, ta có
HB = tan 28\(^o\). OH = tan 28\(^o\). 4 \( \approx \) 2,1 (m)
Vậy chiều cao AB của cây là: AH + HB = 3,6 + 2,1 = 5,7 (m)
Mục 2 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 69 và 70 SGK yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và kỹ năng giải toán.
Bài tập này yêu cầu học sinh xác định hệ số a của hàm số bậc nhất khi biết một điểm thuộc đồ thị hàm số. Để giải bài tập này, học sinh cần thay tọa độ của điểm đã cho vào phương trình hàm số và giải phương trình để tìm ra giá trị của a.
Ví dụ: Cho hàm số y = ax + 2 và điểm A(1; 5) thuộc đồ thị hàm số. Tìm giá trị của a.
Giải:
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị hàm số, học sinh cần xác định ít nhất hai điểm thuộc đồ thị hàm số. Sau đó, nối hai điểm này lại với nhau để được đồ thị hàm số.
Ví dụ: Vẽ đồ thị hàm số y = 2x - 1.
Giải:
Bài tập này yêu cầu học sinh tìm giao điểm của hai đường thẳng. Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình bậc nhất hai ẩn gồm phương trình của hai đường thẳng.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải:
Giải hệ phương trình:
| y = x + 1 | (1) |
| y = -x + 3 | (2) |
Từ (1) và (2) suy ra: x + 1 = -x + 3
Giải phương trình: 2x = 2 => x = 1
Thay x = 1 vào (1) ta được: y = 1 + 1 = 2
Vậy, giao điểm của hai đường thẳng là (1; 2).
Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh đã nắm vững kiến thức và kỹ năng giải các bài tập trong mục 2 trang 69, 70 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!