Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt là với những chủ đề mới.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
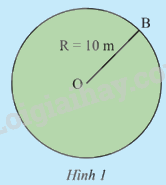
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính: a) Độ dài của toàn bộ hàng rào b) Độ dài của mỗi phần hàng rào c) Độ dài của n phần hàng rào.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 99 SGK Toán 9 Chân trời sáng tạo
Tính độ dài cung 72o của một đường tròn bán kính 25 cm.
Phương pháp giải:
Sử dụng công thức \(l = \frac{{\pi Rn}}{{180}}\).
Lời giải chi tiết:
Cung 72o , bán kính R = 25 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .25.72}}{{180}} \approx 31,42\)cm.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 99SGK Toán 9 Chân trời sáng tạo
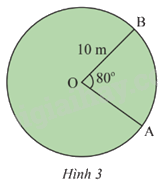
Tính độ dài của của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết \(\widehat {AOB} = {80^o}\).
Phương pháp giải:
- Dựa vào sđ\(\overset\frown{AB}\) = \(\widehat {AOB}\) (\(\overset\frown{AB}\) và góc \(\widehat {AOB}\) cùng chắn cung AB)
- Áp dụng công thức: \(l = \frac{{\pi Rn}}{{180}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {80^o}\), bán kính R = 10 m có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .10.80}}{{180}} \approx 13,96\) (m)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 98SGK Toán 9 Chân trời sáng tạo
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:
a) Độ dài của toàn bộ hàng rào
b) Độ dài của mỗi phần hàng rào
c) Độ dài của n phần hàng rào.
Phương pháp giải:
Dựa vào công thức chu vi hình tròn: C = 2\(\pi \)R .
Lời giải chi tiết:
a) Ta có độ dài của toàn bộ hàng rào là:
C = 2\(\pi \)R = 2.\(\pi \).10 = 20\(\pi \) m
b) Độ dài của mỗi phần hàng rào là:
\(\frac{C}{{360}} = \frac{{20\pi }}{{360}} = \frac{\pi }{{18}}\) m
c) Độ dài của n phần hàng rào là: n.\(\frac{\pi }{{18}}\) m.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 98SGK Toán 9 Chân trời sáng tạo
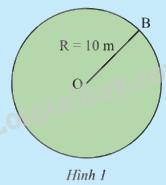
Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:
a) Độ dài của toàn bộ hàng rào
b) Độ dài của mỗi phần hàng rào
c) Độ dài của n phần hàng rào.
Phương pháp giải:
Dựa vào công thức chu vi hình tròn: C = 2\(\pi \)R .
Lời giải chi tiết:
a) Ta có độ dài của toàn bộ hàng rào là:
C = 2\(\pi \)R = 2.\(\pi \).10 = 20\(\pi \) m
b) Độ dài của mỗi phần hàng rào là:
\(\frac{C}{{360}} = \frac{{20\pi }}{{360}} = \frac{\pi }{{18}}\) m
c) Độ dài của n phần hàng rào là: n.\(\frac{\pi }{{18}}\) m.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 99 SGK Toán 9 Chân trời sáng tạo
Tính độ dài cung 72o của một đường tròn bán kính 25 cm.
Phương pháp giải:
Sử dụng công thức \(l = \frac{{\pi Rn}}{{180}}\).
Lời giải chi tiết:
Cung 72o , bán kính R = 25 cm có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .25.72}}{{180}} \approx 31,42\)cm.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 99SGK Toán 9 Chân trời sáng tạo
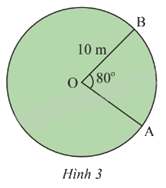
Tính độ dài của của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết \(\widehat {AOB} = {80^o}\).
Phương pháp giải:
- Dựa vào sđ\(\overset\frown{AB}\) = \(\widehat {AOB}\) (\(\overset\frown{AB}\) và góc \(\widehat {AOB}\) cùng chắn cung AB)
- Áp dụng công thức: \(l = \frac{{\pi Rn}}{{180}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {80^o}\), bán kính R = 10 m có độ dài là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .10.80}}{{180}} \approx 13,96\) (m)
Mục 1 trang 98, 99 SGK Toán 9 tập 1 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp hướng dẫn chi tiết, từng bước giải các bài tập, giúp bạn hiểu rõ bản chất của vấn đề và áp dụng kiến thức vào thực tế.
Thông thường, Mục 1 trang 98, 99 sẽ bao gồm các dạng bài tập sau:
Đề bài: (Giả định một đề bài cụ thể từ SGK)
Lời giải:
Đề bài: (Giả định một đề bài cụ thể từ SGK)
Lời giải: (Tương tự như Bài 1)
Để giải bài tập Toán 9 tập 1 - Chân trời sáng tạo một cách hiệu quả, bạn cần lưu ý những điều sau:
Ngoài việc giải các bài tập trong SGK, bạn có thể mở rộng kiến thức bằng cách:
Giải mục 1 trang 98, 99 SGK Toán 9 tập 1 - Chân trời sáng tạo đòi hỏi sự nắm vững kiến thức, kỹ năng và sự kiên trì. Hy vọng rằng với hướng dẫn chi tiết và những lưu ý trên, bạn sẽ tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong môn Toán.