Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 52, 53, 54 sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Bốn ô cửa hình vuông diện tích (frac{1}{2}{m^2}) ghép thành cửa sổ Hình 1. a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 54 SGK Toán 9 Chân trời sáng tạo
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }}\)
b) \( - \frac{{10}}{{3\sqrt 5 }}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\)
Phương pháp giải:
Dựa vào VD3 trang 53 làm tương tự.
Lời giải chi tiết:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }} = \frac{{\sqrt 7 .\sqrt 3 }}{{\sqrt 3 .\sqrt 3 }} = \frac{{\sqrt {21} }}{3}\)
b) \( - \frac{{10}}{{3\sqrt 5 }} = - \frac{{10.\sqrt 5 }}{{3\sqrt 5 .\sqrt 5 }} = - \frac{{10\sqrt 5 }}{{15}}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }} = \frac{{2\sqrt 2 .\sqrt {40} }}{{\sqrt {40} .\sqrt {40} }} = \frac{{8\sqrt 5 }}{{40}} = \frac{{\sqrt 5 }}{5}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\) \( = \frac{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}{\left( {\sqrt 5 - \sqrt 2 } \right).\left( {\sqrt 5 + \sqrt 2 } \right)}\) \( = \frac{\sqrt 2 .\sqrt 5 + \sqrt 2.\sqrt 2 }{{\left( {\sqrt 5 } \right)}^2 - {\left( {\sqrt 2 } \right)^2}}\) \( = \frac{{\sqrt 10 + 2 }}{{5 - 2}}\) \( = \frac{{\sqrt 10 + 2}}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 54 SGK Toán 9 Chân trời sáng tạo
Khử mẫu của các biểu thức lấy căn:
a) \(\sqrt {\frac{{11}}{6}} \)
b) \(a\sqrt {\frac{2}{{5a}}} \) với a > 0
c) \(4x\sqrt {\frac{3}{{4xy}}} \) với x > 0; y > 0
Phương pháp giải:
Dựa vào VD2 trang 53 làm tương tự.
Lời giải chi tiết:
a) \(\sqrt {\frac{{11}}{6}} = \sqrt {\frac{{11.6}}{{6.6}}} = \frac{{\sqrt {66} }}{{\sqrt {{6^2}} }} = \frac{{\sqrt {66} }}{6}\)
b) \(a\sqrt {\frac{2}{{5a}}} = a.\sqrt {\frac{{2.5a}}{{5a.5a}}} = a.\frac{{\sqrt {10a} }}{{\sqrt {{{(5a)}^2}} }} = a.\frac{{\sqrt {10a} }}{{5\left| a \right|}}\)
Vì a > 0 nên \(a.\sqrt {\frac{2}{{5a}}} = a.\frac{{\sqrt {10a} }}{{5a}} = \frac{{\sqrt {10a} }}{{5}}\)
c) \(4x\sqrt {\frac{3}{{4xy}}} = 4x\sqrt {\frac{{3.4xy}}{{4xy.4xy}}} = 4x\frac{{\sqrt {12xy} }}{{\sqrt {{{\left( {4xy} \right)}^2}} }} = \frac{{8x\sqrt {3xy} }}{{\left| {4xy} \right|}}\)
Vì x > 0; y > 0 nên \(4x\sqrt {\frac{3}{{4xy}}} = \frac{{8x\sqrt {3xy} }}{4xy} = \frac{{2\sqrt {3xy} }}{y}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 52 SGK Toán 9 Chân trời sáng tạo
Bốn ô cửa hình vuông diện tích \(\frac{1}{2}{m^2}\) ghép thành cửa sổ Hình 1.
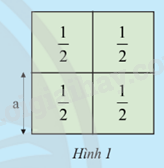
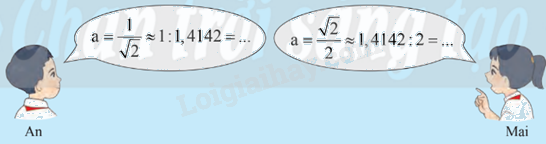
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Kết quả của mỗi bạn có đúng không? Giải thích?
b) Biết rằng \(\sqrt 2 \approx 1,4142\). Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.
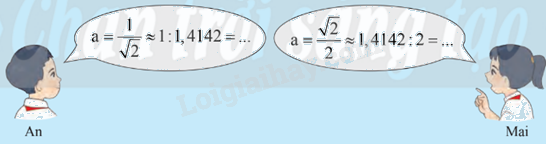
Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?
Phương pháp giải:
Dựa vào diện tích hình vuông: S = a2 với a là độ dài cạnh.
Lời giải chi tiết:
a) Diện tích một hình vuông: S = \(\frac{1}{2}\) (m2)
Mà S = a2 suy ra a = \(\sqrt S = \sqrt {\frac{1}{2}} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) (m)
Vậy kết quả của 2 bạn đều đúng.
b) Theo em, bạn Mai sẽ tìm đáp án nhanh hơn.
Vì phép tính \(1,4142 : 2 \) có số chia là số nguyên nên thực hiện phép chia sẽ dễ hơn phép tính \(1:1,4142\) có số chia là số thập phân
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 54SGK Toán 9 Chân trời sáng tạo
Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.
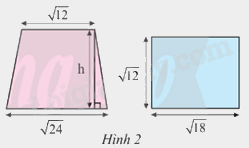
Phương pháp giải:
Dựa vào công thức diện tích hình chữ nhật S = a.b (a: chiều dài; b: chiều rộng), diện tích hình thang S = \(\frac{1}{2}(a + b).h\) (a và b: chiều dài hai cạnh đáy; h: chiều cao).
Lời giải chi tiết:
Ta có diện tích hình chữ nhật là: \(\sqrt {12} .\sqrt {18} = \sqrt {12.18} = \sqrt {216} = 6\sqrt 6 \)
Ta có diện tích hình thang bằng diện tích hình chữ nhật là: \(6\sqrt 6 \)
Mà diện tích hình thang là: \(\frac{1}{2}(\sqrt {12} + \sqrt {24} ).h\) = \(6\sqrt 6 \)
Suy ra h = \(\frac{{2.6\sqrt 6 }}{{(\sqrt {12} + \sqrt {24} )}} = 12 - 6\sqrt 2 \)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 52 SGK Toán 9 Chân trời sáng tạo
Bốn ô cửa hình vuông diện tích \(\frac{1}{2}{m^2}\) ghép thành cửa sổ Hình 1.
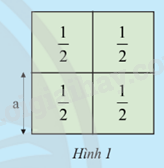
a) Hai bạn An và Mai tính độ dài cạnh a (m) của mỗi ô cửa.

Kết quả của mỗi bạn có đúng không? Giải thích?
b) Biết rằng \(\sqrt 2 \approx 1,4142\). Không dùng máy tính cầm tay, hai bạn tìm giá trị gần đúng của độ dài mỗi ô cửa.
Theo em, bạn nào sẽ tìm ra đáp án nhanh hơn?
Phương pháp giải:
Dựa vào diện tích hình vuông: S = a2 với a là độ dài cạnh.
Lời giải chi tiết:
a) Diện tích một hình vuông: S = \(\frac{1}{2}\) (m2)
Mà S = a2 suy ra a = \(\sqrt S = \sqrt {\frac{1}{2}} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\) (m)
Vậy kết quả của 2 bạn đều đúng.
b) Theo em, bạn Mai sẽ tìm đáp án nhanh hơn.
Vì phép tính \(1,4142 : 2 \) có số chia là số nguyên nên thực hiện phép chia sẽ dễ hơn phép tính \(1:1,4142\) có số chia là số thập phân
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 54 SGK Toán 9 Chân trời sáng tạo
Trục căn thức ở mẫu các biểu thức sau:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }}\)
b) \( - \frac{{10}}{{3\sqrt 5 }}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\)
Phương pháp giải:
Dựa vào VD3 trang 53 làm tương tự.
Lời giải chi tiết:
a) \(\frac{{\sqrt 7 }}{{\sqrt 3 }} = \frac{{\sqrt 7 .\sqrt 3 }}{{\sqrt 3 .\sqrt 3 }} = \frac{{\sqrt {21} }}{3}\)
b) \( - \frac{{10}}{{3\sqrt 5 }} = - \frac{{10.\sqrt 5 }}{{3\sqrt 5 .\sqrt 5 }} = - \frac{{10\sqrt 5 }}{{15}}\)
c) \(\frac{{2\sqrt 2 }}{{\sqrt {40} }} = \frac{{2\sqrt 2 .\sqrt {40} }}{{\sqrt {40} .\sqrt {40} }} = \frac{{8\sqrt 5 }}{{40}} = \frac{{\sqrt 5 }}{5}\)
d) \(\frac{{\sqrt 2 }}{{\sqrt 5 - \sqrt 2 }}\) \( = \frac{\sqrt 2 .\left( {\sqrt 5 + \sqrt 2 } \right)}{\left( {\sqrt 5 - \sqrt 2 } \right).\left( {\sqrt 5 + \sqrt 2 } \right)}\) \( = \frac{\sqrt 2 .\sqrt 5 + \sqrt 2.\sqrt 2 }{{\left( {\sqrt 5 } \right)}^2 - {\left( {\sqrt 2 } \right)^2}}\) \( = \frac{{\sqrt 10 + 2 }}{{5 - 2}}\) \( = \frac{{\sqrt 10 + 2}}{3}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 54 SGK Toán 9 Chân trời sáng tạo
Khử mẫu của các biểu thức lấy căn:
a) \(\sqrt {\frac{{11}}{6}} \)
b) \(a\sqrt {\frac{2}{{5a}}} \) với a > 0
c) \(4x\sqrt {\frac{3}{{4xy}}} \) với x > 0; y > 0
Phương pháp giải:
Dựa vào VD2 trang 53 làm tương tự.
Lời giải chi tiết:
a) \(\sqrt {\frac{{11}}{6}} = \sqrt {\frac{{11.6}}{{6.6}}} = \frac{{\sqrt {66} }}{{\sqrt {{6^2}} }} = \frac{{\sqrt {66} }}{6}\)
b) \(a\sqrt {\frac{2}{{5a}}} = a.\sqrt {\frac{{2.5a}}{{5a.5a}}} = a.\frac{{\sqrt {10a} }}{{\sqrt {{{(5a)}^2}} }} = a.\frac{{\sqrt {10a} }}{{5\left| a \right|}}\)
Vì a > 0 nên \(a.\sqrt {\frac{2}{{5a}}} = a.\frac{{\sqrt {10a} }}{{5a}} = \frac{{\sqrt {10a} }}{{5}}\)
c) \(4x\sqrt {\frac{3}{{4xy}}} = 4x\sqrt {\frac{{3.4xy}}{{4xy.4xy}}} = 4x\frac{{\sqrt {12xy} }}{{\sqrt {{{\left( {4xy} \right)}^2}} }} = \frac{{8x\sqrt {3xy} }}{{\left| {4xy} \right|}}\)
Vì x > 0; y > 0 nên \(4x\sqrt {\frac{3}{{4xy}}} = \frac{{8x\sqrt {3xy} }}{4xy} = \frac{{2\sqrt {3xy} }}{y}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 54SGK Toán 9 Chân trời sáng tạo
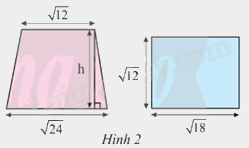
Biết rằng hình thang và hình chữ nhật ở Hình 2 có diện tích bằng nhau. Tính chiều cao h của hình thang.
Phương pháp giải:
Dựa vào công thức diện tích hình chữ nhật S = a.b (a: chiều dài; b: chiều rộng), diện tích hình thang S = \(\frac{1}{2}(a + b).h\) (a và b: chiều dài hai cạnh đáy; h: chiều cao).
Lời giải chi tiết:
Ta có diện tích hình chữ nhật là: \(\sqrt {12} .\sqrt {18} = \sqrt {12.18} = \sqrt {216} = 6\sqrt 6 \)
Ta có diện tích hình thang bằng diện tích hình chữ nhật là: \(6\sqrt 6 \)
Mà diện tích hình thang là: \(\frac{1}{2}(\sqrt {12} + \sqrt {24} ).h\) = \(6\sqrt 6 \)
Suy ra h = \(\frac{{2.6\sqrt 6 }}{{(\sqrt {12} + \sqrt {24} )}} = 12 - 6\sqrt 2 \)
Mục 1 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 52, 53, 54 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và kỹ năng giải toán.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, xác định hệ số a, b của hàm số y = ax + b và vẽ đồ thị hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc nhất, các yếu tố ảnh hưởng đến đồ thị hàm số và cách xác định các điểm thuộc đồ thị.
Bài 2 yêu cầu học sinh xác định hàm số bậc nhất khi biết các yếu tố như hệ số góc, điểm thuộc đồ thị hoặc hai điểm thuộc đồ thị. Để giải bài tập này, học sinh cần sử dụng các công thức và phương pháp đã học để tìm ra các hệ số a, b của hàm số.
Bài 3 yêu cầu học sinh tìm giao điểm của hai đường thẳng bằng phương pháp giải hệ phương trình. Để giải bài tập này, học sinh cần nắm vững phương pháp giải hệ phương trình bậc nhất hai ẩn và áp dụng vào việc tìm tọa độ giao điểm của hai đường thẳng.
Bài 4 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế như tính quãng đường, thời gian, vận tốc. Để giải bài tập này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số và xây dựng phương trình toán học để giải quyết bài toán.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!