Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 5 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải chi tiết, giúp các em học sinh có thể tự học tại nhà hoặc ôn tập kiến thức một cách hiệu quả.
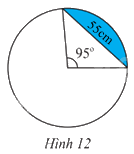
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung số đo là 95o. (Hình 12).
Đề bài
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung số đo là 95o. (Hình 12).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tính diện tích tam giác OAB.
- Tính diện tích hình quạt tròn OamB.
- Tính diện tích hình viên phân AmB = diện tích hình quạt tròn OamB - diện tích tam giác OAB.
Lời giải chi tiết
Gọi các điểm như hình dưới:
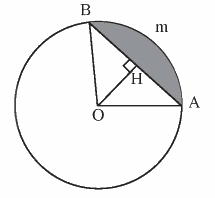
Gọi AmB là hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo $95^\circ$.
Vẽ $OH \perp AB$ tại $H$. Khi đó $H$ là trung điểm của $AB$.
Suy ra $AH = BH = \frac{AB}{2} = \frac{55}{2} = 27,5 \text{ (cm)}.$
Ta có $OA = OB = R$ nên $\Delta OAB$ cân tại $O$.
Mà $OH \perp AB$ nên $OH$ là tia phân giác của góc $AOB$, suy ra $\widehat {AOH} = \frac{\widehat {AOB}}{2} = \frac{95^\circ}{2} = 47,5^\circ.$
Áp dụng hệ thức giữa cạnh và góc trong $\Delta AOH$ vuông tại $H$, ta có:
$OH = AH \cdot \cot \widehat {AOH} = 27,5 \cdot \cot 47,5^\circ \approx 25,2 \text{ (cm)}; $
$OA = \frac{AH}{\sin \widehat {AOH}} = \frac{27,5}{\sin 47,5^\circ} \approx 37,3 \text{ (cm)}. $
Diện tích của tam giác $OAB$ là:
$S_{OAB} = \frac{1}{2} \cdot OH \cdot AB = \frac{1}{2} \cdot 25,2 \cdot 55 \approx 693 \text{ (cm}^2). \quad (1) $
Diện tích hình quạt tròn $OAmB$ là:
$S_{OAmB} = \frac{\pi R^2 n}{360} \approx \frac{\pi \cdot (37,3)^2 \cdot 95}{360} \approx 1153,42 \text{ (cm}^2). \quad (2) $
Từ $(1)$ và $(2)$ suy ra diện tích hình viên phân $AmB$ là:
$S_{AmB} = S_{OAmB} - S_{OAB} \approx 1153,42 - 693 \approx 460,42 \text{ (cm}^2). $
Bài tập 5 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song.
Bài tập 5 bao gồm các ý nhỏ khác nhau, mỗi ý yêu cầu học sinh thực hiện một thao tác cụ thể liên quan đến hàm số bậc nhất. Cụ thể:
Để giải bài tập 5 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Ý a: Để xác định hệ số góc của đường thẳng, ta cần đưa phương trình đường thẳng về dạng y = ax + b. Sau đó, hệ số góc của đường thẳng là giá trị của a.
Ví dụ: Cho đường thẳng 2x + 3y = 6. Để đưa về dạng y = ax + b, ta thực hiện các bước sau:
Ý b: Để xác định đường thẳng song song với một đường thẳng cho trước, ta cần đảm bảo rằng hệ số góc của hai đường thẳng bằng nhau. Sau đó, ta có thể chọn một giá trị tùy ý cho tung độ gốc để xác định phương trình đường thẳng.
Ví dụ: Tìm đường thẳng song song với đường thẳng y = 2x + 1. Ta có thể chọn đường thẳng y = 2x + 3, y = 2x - 5, hoặc bất kỳ đường thẳng nào có hệ số góc là 2.
Ý c: Để tìm giá trị của tham số để đường thẳng thỏa mãn một điều kiện nhất định, ta cần thay điều kiện đó vào phương trình đường thẳng và giải phương trình để tìm giá trị của tham số.
Ví dụ: Tìm giá trị của m để đường thẳng y = (m - 1)x + 2 đi qua điểm A(1; 3). Ta thay x = 1 và y = 3 vào phương trình đường thẳng:
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập sau:
Bài tập 5 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.