Định lí Viète là một trong những kiến thức quan trọng của chương trình Toán 9, đặc biệt trong sách Chân trời sáng tạo. Nắm vững định lí này giúp học sinh giải quyết các bài toán liên quan đến phương trình bậc hai một cách hiệu quả.
Bài viết này sẽ cung cấp đầy đủ lý thuyết, các dạng bài tập thường gặp và phương pháp giải chi tiết, giúp bạn hiểu sâu sắc và áp dụng thành thạo Định lí Viète.
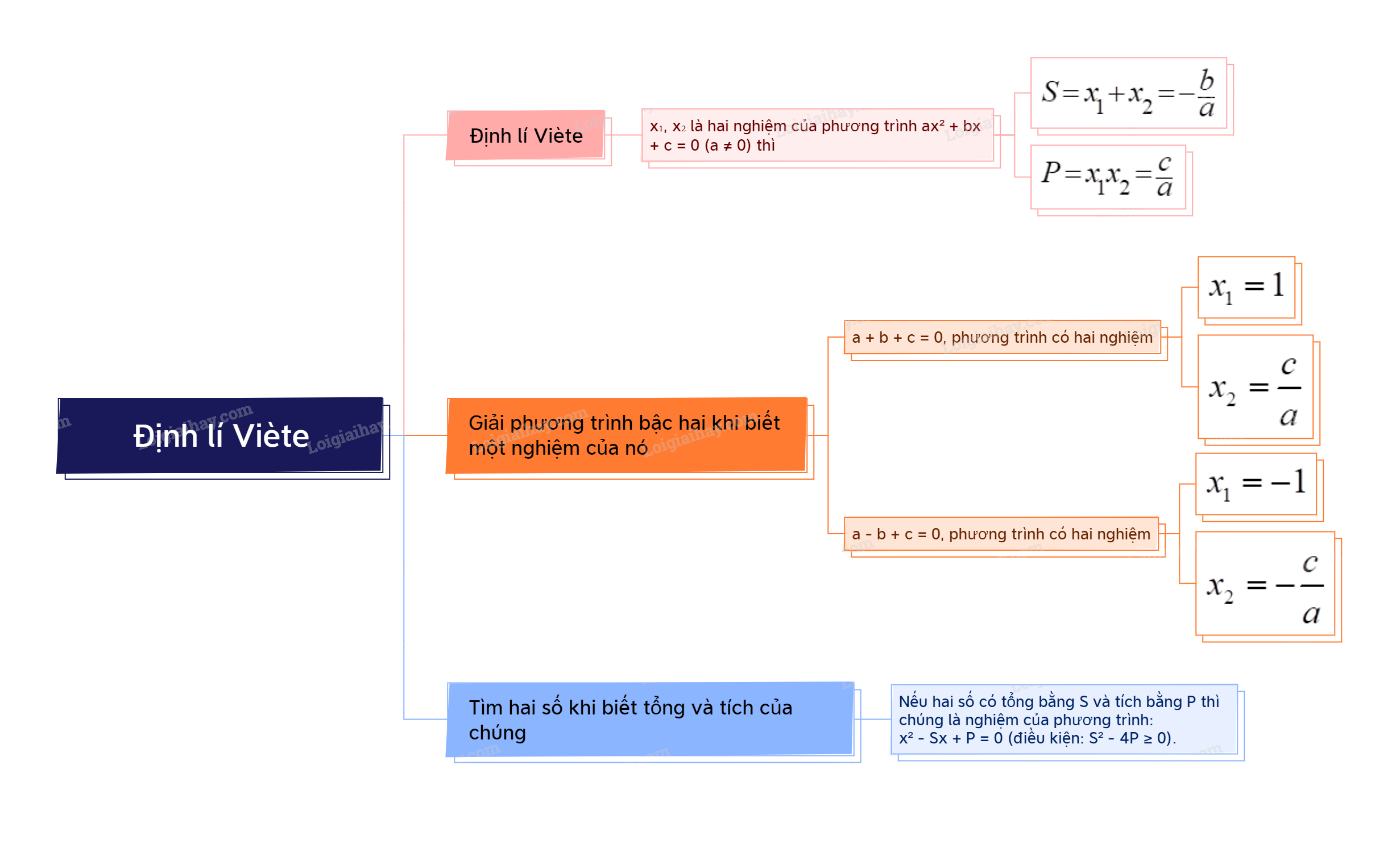
1. Định lí Viète Định lí Viète Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},{x_2}\) thì tổng và tích của hai nghiệm đó là \(S = {x_1} + {x_2} = - \frac{b}{a};P = {x_1}{x_2} = \frac{c}{a}.\)
1. Định lí Viète
Định lí Viète
Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},{x_2}\) thì tổng và tích của hai nghiệm đó là \(S = {x_1} + {x_2} = - \frac{b}{a};P = {x_1}{x_2} = \frac{c}{a}.\) |
Ví dụ: Phương trình \(2{x^2} + 11x + 7 = 0\) có: \(\Delta = {11^2} - 4.2.7 = 65 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{11}}{2};{x_1}{x_2} = \frac{7}{2}\).
Giải phương trình bậc hai khi biết một nghiệm của nó
Xét phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). - Nếu \(a + b + c = 0\) thì phương trình có một nghiệm là \({x_1} = 1\), còn nghiệm kia là \({x_2} = \frac{c}{a}\). - Nếu \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1} = - 1\), còn nghiệm kia là \({x_2} = - \frac{c}{a}\). |
Ví dụ: Phương trình \({x^2} - 6x + 5 = 0\) có \(a + b + c = 1 + \left( { - 6} \right) + 5 = 0\) nên phương trình có hai nghiệm: \({x_1} = 1,{x_2} = 5\).
Phương trình \(5{x^2} + 14x + 9 = 0\) có \(a - b + c = 5 - 14 + 9 = 0\) nên phương trình có hai nghiệm: \({x_1} = - 1,{x_2} = - \frac{9}{5}\).
2. Tìm hai số khi biết tổng và tích của chúng
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: \({x^2} - Sx + P = 0\). Điều kiện để có hai số đó là \({S^2} - 4P \ge 0\). |
Ví dụ: Hai số có tổng bằng 9, tích bằng 20 là nghiệm của phương trình \({x^2} + 9x + 20 = 0\).
Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.1.20 = 1,\sqrt \Delta = 1\).
Suy ra phương trình có hai nghiệm \({x_1} = \frac{{9 - 1}}{2} = 4;{x_2} = \frac{{9 + 1}}{2} = 5\).
Vậy hai số cần tìm là 4 và 5.
Định lí Viète là một công cụ mạnh mẽ trong việc nghiên cứu và giải quyết các phương trình bậc hai. Nó thiết lập mối liên hệ giữa các hệ số của phương trình và các nghiệm của nó. Trong chương trình Toán 9 Chân trời sáng tạo, việc hiểu rõ và vận dụng Định lí Viète là yếu tố then chốt để đạt kết quả tốt.
Phương trình bậc hai tổng quát có dạng: ax2 + bx + c = 0 (với a ≠ 0). Nghiệm của phương trình là giá trị của x thỏa mãn phương trình. Để tìm nghiệm, ta thường sử dụng công thức nghiệm:
x1,2 = (-b ± √(b2 - 4ac)) / 2a
Biệt thức Δ = b2 - 4ac đóng vai trò quan trọng trong việc xác định số nghiệm của phương trình:
Định lí Viète phát biểu rằng:
Nếu phương trình bậc hai ax2 + bx + c = 0 (với a ≠ 0) có hai nghiệm x1 và x2 thì:
Đặc biệt, nếu a = 1, phương trình trở thành x2 + bx + c = 0, khi đó:
Định lí Viète có nhiều ứng dụng quan trọng trong việc giải toán:
Ví dụ 1: Cho phương trình x2 - 5x + 6 = 0. Tìm tổng và tích của các nghiệm.
Ta có a = 1, b = -5, c = 6. Áp dụng Định lí Viète:
Ví dụ 2: Cho phương trình 2x2 + 4x - 6 = 0. Tìm tổng và tích của các nghiệm.
Ta có a = 2, b = 4, c = -6. Áp dụng Định lí Viète:
Hãy tự giải các bài tập sau để củng cố kiến thức về Định lí Viète:
Khi áp dụng Định lí Viète, cần chú ý đến dấu của các hệ số a, b, c để tính toán chính xác tổng và tích của các nghiệm. Ngoài ra, cần kiểm tra điều kiện có nghiệm của phương trình trước khi áp dụng Định lí Viète.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về Lý thuyết Định lí Viète Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!