Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 9 tập 1 - Chân trời sáng tạo, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 10, 11, 12. Các em có thể tham khảo lời giải để hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Để chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức: (y = frac{5}{9}(x - 32)) a) Biến đổi công thức trên về dạng x – 1,8y = 32. (1) b) Hỏi 20oC tương ứng bao nhiêu độ F? c) Hỏi 98,6oF tương ứng bao nhiêu độ C?
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 9 Chân trời sáng tạo
Để chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức:
\(y = \frac{5}{9}(x - 32)\)
a) Biến đổi công thức trên về dạng x – 1,8y = 32.(1)
b) Hỏi 20oC tương ứng bao nhiêu độ F?
c) Hỏi 98,6oF tương ứng bao nhiêu độ C?
Phương pháp giải:
- Biến đổi cho x,y về cùng 1 vế, hằng số 1 vế
- Rút x theo y thay vào tính ra kết quả rồi kết luận
- Rút y theo x thay vào tính ra kết quả rồi kết luận
Lời giải chi tiết:
a) Ta có \(y = \frac{5}{9}(x - 32)\)
\(9y = 5(x - 32)\)
\(\begin{array}{l}5x - 9y = 160\\x - 1,8y = 32\end{array}\)
b) x – 1,8y = 32
\(\begin{array}{l}x = 32 + 1,8y\\x = 32 + 1,8.20\\x = 68\end{array}\)
Vậy 20oC tương ứng 68oF.
c) Ta có \(y = \frac{5}{9}(x - 32)\)
\(y = \frac{5}{9}(98,6 - 32) = 37\)
Vậy 98,6oF tương ứng 37oC.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 12 SGK Toán 9 Chân trời sáng tạo
Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau:
a) x + 5y = -4
b) \(\sqrt 3 x + y = 0\)
c) \(0x - \frac{3}{2}y = 6\)
d) 2x + 0y = - 1,5.
Phương pháp giải:
Dựa vào khái niệm phương trình bậc nhất hai ẩn x và y là hệ thức có dạng
\(ax + by = c\)
Trong đó, a và b không đồng thời bằng 0.
Lời giải chi tiết:
a) a = 1; b = 5; c = -4
b) a = \(\sqrt 3 \); b = 1; c = 0
c) a = 0; b = \( - \frac{3}{2}\); c = 6
d) a = 2; b = 0; c = - 1,5.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 12 SGK Toán 9 Chân trời sáng tạo
Cho phương trình 3x + 2y = 4. (1)
a) Trong 2 cặp số (1;2) và (2;-1), cặp số nào là nghiệm của phương trình(1)?
b) Tìm yo để cặp số (4;yo) là nghiệm của phương trình (1).
c) Tìm thêm 2 nghiệm của phương trình (1).
d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng toạ độ Oxy.
Phương pháp giải:
- Thay lần lượt 2 cặp số vào phương trình (1) cái nào thoả mãn thì chính là nghiệm.
- Thay x = 4 và phương trình để tìm ra yo.
- Cho x bất kì rồi tìm ra y
- Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy.
Lời giải chi tiết:
a) Thay cặp số (1;2) vào (1) ta có:
3.1 + 2.2 = 7 \( \ne \) VP. Vậy (1;2) không phải nghiệm của (1)
Thay cặp số (2;-1) vào (1) ta có: 3.2 + 2.(-1) = 4 = VP. Vậy (2;-1) là nghiệm của (1).
b) Thay x = 4 vào (1) ta có:
3.4 + 2y = 4
Suy ra \({y_o} = \frac{{4 - 12}}{2} = - 4\).
c) Ta có
\(\begin{array}{l}3x + 2y = 4\\y = \frac{{4 - 3x}}{2}\end{array}\)
Cho x = 0 suy ra \(y = 2\). Vậy (0;2) là nghiệm của phương trình (1).
Cho x = 1 suy ra \(y = \frac{1}{2}\). Vậy (1; \(\frac{1}{2}\)) là nghiệm của phương trình (1).
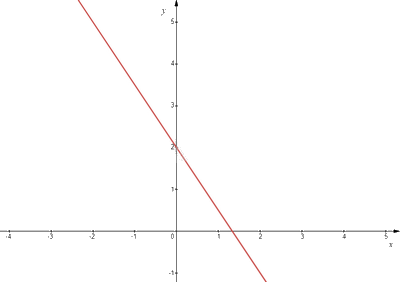
d) Viết lại phương trình thành \(y = \frac{{4 - 3x}}{2} = 2 - \frac{3}{2}x\). Từ đó, tất cả các nghiệm đã cho được biểu diễn bởi đường thẳng d: \(y = 2 - \frac{3}{2}x\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 10 SGK Toán 9 Chân trời sáng tạo
Để chuyển đổi từ độ F ( kí hiệu x) sang độ C (ký hiệu y), ta dùng công thức:
\(y = \frac{5}{9}(x - 32)\)
a) Biến đổi công thức trên về dạng x – 1,8y = 32.(1)
b) Hỏi 20oC tương ứng bao nhiêu độ F?
c) Hỏi 98,6oF tương ứng bao nhiêu độ C?
Phương pháp giải:
- Biến đổi cho x,y về cùng 1 vế, hằng số 1 vế
- Rút x theo y thay vào tính ra kết quả rồi kết luận
- Rút y theo x thay vào tính ra kết quả rồi kết luận
Lời giải chi tiết:
a) Ta có \(y = \frac{5}{9}(x - 32)\)
\(9y = 5(x - 32)\)
\(\begin{array}{l}5x - 9y = 160\\x - 1,8y = 32\end{array}\)
b) x – 1,8y = 32
\(\begin{array}{l}x = 32 + 1,8y\\x = 32 + 1,8.20\\x = 68\end{array}\)
Vậy 20oC tương ứng 68oF.
c) Ta có \(y = \frac{5}{9}(x - 32)\)
\(y = \frac{5}{9}(98,6 - 32) = 37\)
Vậy 98,6oF tương ứng 37oC.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 12 SGK Toán 9 Chân trời sáng tạo
Xác định các hệ số a, b, c của mỗi phương trình bậc nhất hai ẩn sau:
a) x + 5y = -4
b) \(\sqrt 3 x + y = 0\)
c) \(0x - \frac{3}{2}y = 6\)
d) 2x + 0y = - 1,5.
Phương pháp giải:
Dựa vào khái niệm phương trình bậc nhất hai ẩn x và y là hệ thức có dạng
\(ax + by = c\)
Trong đó, a và b không đồng thời bằng 0.
Lời giải chi tiết:
a) a = 1; b = 5; c = -4
b) a = \(\sqrt 3 \); b = 1; c = 0
c) a = 0; b = \( - \frac{3}{2}\); c = 6
d) a = 2; b = 0; c = - 1,5.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 12 SGK Toán 9 Chân trời sáng tạo
Cho phương trình 3x + 2y = 4. (1)
a) Trong 2 cặp số (1;2) và (2;-1), cặp số nào là nghiệm của phương trình(1)?
b) Tìm yo để cặp số (4;yo) là nghiệm của phương trình (1).
c) Tìm thêm 2 nghiệm của phương trình (1).
d) Hãy biểu diễn tất cả các nghiệm của phương trình (1) trên mặt phẳng toạ độ Oxy.
Phương pháp giải:
- Thay lần lượt 2 cặp số vào phương trình (1) cái nào thoả mãn thì chính là nghiệm.
- Thay x = 4 và phương trình để tìm ra yo.
- Cho x bất kì rồi tìm ra y
- Dựa vào VD3 trang 11 để vẽ các nghiệm trên mặt phẳng toạ độ Oxy.
Lời giải chi tiết:
a) Thay cặp số (1;2) vào (1) ta có:
3.1 + 2.2 = 7 \( \ne \) VP. Vậy (1;2) không phải nghiệm của (1)
Thay cặp số (2;-1) vào (1) ta có: 3.2 + 2.(-1) = 4 = VP. Vậy (2;-1) là nghiệm của (1).
b) Thay x = 4 vào (1) ta có:
3.4 + 2y = 4
Suy ra \({y_o} = \frac{{4 - 12}}{2} = - 4\).
c) Ta có
\(\begin{array}{l}3x + 2y = 4\\y = \frac{{4 - 3x}}{2}\end{array}\)
Cho x = 0 suy ra \(y = 2\). Vậy (0;2) là nghiệm của phương trình (1).
Cho x = 1 suy ra \(y = \frac{1}{2}\). Vậy (1; \(\frac{1}{2}\)) là nghiệm của phương trình (1).
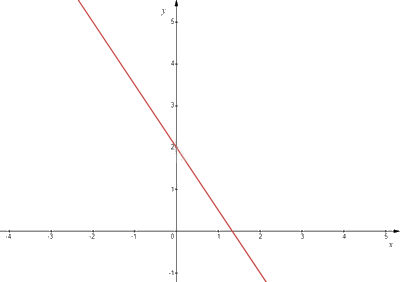
d) Viết lại phương trình thành \(y = \frac{{4 - 3x}}{2} = 2 - \frac{3}{2}x\). Từ đó, tất cả các nghiệm đã cho được biểu diễn bởi đường thẳng d: \(y = 2 - \frac{3}{2}x\).
Mục 1 của SGK Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Đây là nền tảng quan trọng để học sinh tiếp cận các kiến thức nâng cao hơn trong chương trình Toán 9. Việc nắm vững các khái niệm, tính chất và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Bài 1 yêu cầu học sinh xác định hệ số góc của các hàm số bậc nhất cho trước. Để giải bài này, học sinh cần nhớ lại định nghĩa về hệ số góc của hàm số y = ax + b, đó là giá trị của a. Ví dụ, với hàm số y = 2x - 3, hệ số góc là 2.
Bài 2 yêu cầu học sinh vẽ đồ thị của các hàm số bậc nhất. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Có thể chọn điểm giao với trục x (y = 0) và điểm giao với trục y (x = 0). Sau đó, nối hai điểm này lại để được đồ thị của hàm số.
Bài 3 là một bài toán ứng dụng, yêu cầu học sinh giải quyết một tình huống thực tế liên quan đến hàm số bậc nhất. Để giải bài này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số và xây dựng phương trình toán học để giải quyết vấn đề.
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý các điểm sau:
Việc giải bài tập mục 1 trang 10, 11, 12 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bước quan trọng trong quá trình học tập môn Toán 9. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài toán về hàm số bậc nhất và đạt kết quả tốt trong học tập.