Bài 10 trang 108 sách bài tập Toán 9 Cánh diều tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số, tìm đỉnh của parabol, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 108 SBT Toán 9 Cánh diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác đều ABC cạnh a. Vẽ về phía ngoài tam giác ABC các hình chữ nhật ABEF, BCIJ và CAGH sao cho AF = BJ = CH = x. Tìm hệ thức liên hệ giữa a2 và x2 để hình lục giác EFGHIJ là lục giác đều.
Đề bài
Cho tam giác đều ABC cạnh a. Vẽ về phía ngoài tam giác ABC các hình chữ nhật ABEF, BCIJ và CAGH sao cho AF = BJ = CH = x. Tìm hệ thức liên hệ giữa a2 và x2 để hình lục giác EFGHIJ là lục giác đều.
Phương pháp giải - Xem chi tiết
Dựa vào dữ kiện đề bài để vẽ hình.
Dựa vào đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
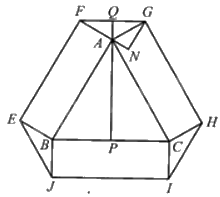
Gọi P là trung điểm của BC và Q là giao điểm của các đường thẳng AP và FG.
Xét ∆ABC đều có AP là đường trung tuyến nên đồng thời là đường phân giác của tam giác.
Do đó: \(\widehat {BAP} = \widehat {PAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}{.60^o} = {30^o}\).
Xét ∆AFG cân tại A (do AF = AG = x) nên đường trung tuyến AQ đồng thời là đường phân giác của tam giác. Do đó \(\widehat {FAG} = 2\widehat {PAQ}\).
Lại có: \(\widehat {PAQ} + \widehat {FAB} + \widehat {BAP} = {180^o}\)
Nên \(\widehat {PAQ} = {180^o} - \widehat {FAB} - \widehat {BAP}\) \( = {180^o} - {90^o} - {30^o} = {60^o}\).
Suy ra \(\widehat {PAG} = 2.\widehat {PAQ} = {2.60^o} = {120^o}\).
Kẻ GN vuông góc với FA (N thuộc FA).
Tam giác FQA vuông tại Q có \(\widehat {FAQ} = {60^o}\) và FA = x nên ta có:
\(FQ = FA.\sin \widehat {FAQ} = \frac{{x\sqrt 3 }}{2}\), do đó FG = 2FQ = \(x\sqrt 3 \).
Do ABEF, BCIJ và CAGH là các hình chữ nhật nên ta có: AB = EF, BC = IJ, CA = GH, mà AB = BC = CA (do ∆ABC đều) nên nếu EFGHIJ là lục giác đều thì FG = GH = AC = a, do đó a = \(x\sqrt 3 \) hay a2 = 3x2.
Ngược lại, nếu a2 = 3x2 thì FG = a và các cạnh của lục giác EFGHIJ bằng nhau. (1)
Ta có \(\widehat {AFQ} + \widehat {FAQ} = {90^o}\)(do ∆AFQ vuông tại Q) nên:
\(\widehat {AFQ} = {90^o} - \widehat {FAQ} = {90^o} - {60^o} = {30^o}\)
Suy ra \(\widehat {EFQ} = \widehat {EFA} + \widehat {AFQ} = {90^o} + {30^o} = {120^o}\).
Tương tự, ta chứng minh được các góc của lục giác EFGHIJ đều bằng 120° nên lục giác EFGHIJ là lục giác đều.
Vậy hệ thức liên hệ giữa a2 và x2 để lục giác EFGHIJ là lục giác đều là a2 = 3x2.
Bài 10 trang 108 sách bài tập Toán 9 Cánh diều tập 2 yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc hai. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Để giải bài 10 trang 108 SBT Toán 9 Cánh diều tập 2, chúng ta thực hiện theo các bước sau:
Giả sử hàm số được cho là y = x2 - 4x + 3. Ta thực hiện các bước sau:
Để rèn luyện thêm kỹ năng giải bài tập về hàm số bậc hai, các em có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 2 hoặc trên các trang web học toán online.
Bài 10 trang 108 sách bài tập Toán 9 Cánh diều tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc hai. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.