Bài 19 trang 87 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 19 trang 87 Sách bài tập Toán 9 - Cánh Diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một khối u (ở vị trí A) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia (ở vị trí B) cách hình chiếu của khối u (ở vị trí C) trên da mặt là 8,3 cm (Hình 19). a) Hỏi góc tạo bởi chùm tia gamma với da mặt là bao nhiêu độ (làm tròn kết quả đến hàng phần mười)? b) Chùm tia phải đi một đoạn dài bao nhiêu centimét để đến được khối u (làm tròn kết quả đến hàng phần mười).
Đề bài
Một khối u (ở vị trí A) của một bệnh nhân cách da mặt 5,7 cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia (ở vị trí B) cách hình chiếu của khối u (ở vị trí C) trên da mặt là 8,3 cm (Hình 19).
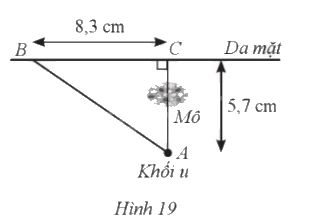
a) Hỏi góc tạo bởi chùm tia gamma với da mặt là bao nhiêu độ (làm tròn kết quả đến hàng phần mười)?
b) Chùm tia phải đi một đoạn dài bao nhiêu centimét để đến được khối u (làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
a) Góc tạo bởi chùm tia gamma với da mặt là góc B.
b) Độ dài đoạn thẳng cần tìm là AB.
Lời giải chi tiết
Ta có: Độ dài đường đi của chùm tia gamma tới khối u là AB; góc tạo bởi chùm tia gamma với da mặt là góc ABC.
a) Xét tam giác ABC vuông tại C ta có: \(\tan \widehat {ABC} = \frac{{AC}}{{BC}} = \frac{{5,7}}{{8,3}} = \frac{{57}}{{83}}\).
Suy ra \(\widehat {ABC} = 34,5^\circ \).
Vậy góc tạo bởi chùm tia gamma với da mặt là \(34,5^\circ \).
b) Xét tam giác ABC vuông tại C ta có \(AB = \sqrt {A{C^2} + B{C^2}} = \sqrt {5,{7^2} + 8,{3^2}} \approx 10,1\)cm.
Vậy chùm tia phải đi một đoạn dài 10,1cm để đến được khối u.
Bài 19 trang 87 Sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định hệ số góc, điểm thuộc đồ thị hàm số, và giải các bài toán liên quan đến ứng dụng của hàm số trong thực tế.
Bài 19 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào các kiến thức sau:
Giả sử câu a yêu cầu xác định hệ số góc của hàm số y = 2x - 3. Hệ số góc của hàm số này là a = 2.
Giả sử câu b yêu cầu vẽ đồ thị hàm số y = -x + 1. Để vẽ đồ thị, ta cần xác định hai điểm thuộc đồ thị, ví dụ: (0, 1) và (1, 0). Sau đó, nối hai điểm này lại với nhau để được đồ thị hàm số.
Giả sử câu c là một bài toán ứng dụng: Một ô tô đi từ A đến B với vận tốc 60km/h. Hãy viết hàm số biểu thị quãng đường đi được của ô tô theo thời gian.
Gọi s là quãng đường đi được (km) và t là thời gian đi (giờ). Hàm số biểu thị quãng đường đi được là s = 60t.
Ngoài bài 19, các em học sinh cũng nên tìm hiểu thêm về các ứng dụng của hàm số trong các lĩnh vực khác nhau của đời sống, như kinh tế, vật lý, và kỹ thuật.
Bài 19 trang 87 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến hàm số.