Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 16 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.
Đề bài
Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {AEB} = \widehat {AEC} = {60^o}\)suy ra EA là phân giác của góc BEC.
Lời giải chi tiết
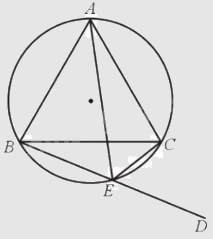
Ta có tứ giác ABEC nội tiếp đường tròn nên \(\widehat {CED} = \widehat {BAC} = {60^o}( = {180^o} - \widehat {BEC})\). Mặt khác \(\widehat {AEC} = \widehat {CED} = {60^o}\). Do đó, EC là phân giác của góc AED.
Tương tự ta có \(\widehat {AEC} = \widehat {ABC} = {60^o}\) và \(\widehat {AEB} = \widehat {ACB} = {60^o}\).
Do đó \(\widehat {AEB} = \widehat {AEC} = {60^o}\) hay EA là phân giác của góc BEC.
Bài 16 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số, và cách xác định phương trình đường thẳng.
Bài 16 bao gồm các câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để xác định hệ số góc của đường thẳng, ta sử dụng công thức: y = ax + b, trong đó a là hệ số góc. Học sinh cần nắm vững cách xác định a từ phương trình đường thẳng hoặc từ hai điểm thuộc đường thẳng.
Ví dụ: Cho đường thẳng y = 2x - 3, hệ số góc của đường thẳng này là a = 2.
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình gồm phương trình của hai đường thẳng đó. Hoành độ và tung độ của nghiệm của hệ phương trình chính là tọa độ giao điểm của hai đường thẳng.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải hệ phương trình:
x + 1 = -x + 32x = 2x = 1Thay x = 1 vào phương trình y = x + 1, ta được y = 2. Vậy giao điểm của hai đường thẳng là (1; 2).
Có nhiều cách để viết phương trình đường thẳng. Một trong những cách phổ biến nhất là sử dụng công thức:
y - y1 = m(x - x1), trong đó (x1; y1) là tọa độ của một điểm thuộc đường thẳng và m là hệ số góc.
Ví dụ: Viết phương trình đường thẳng đi qua điểm (2; 3) và có hệ số góc m = 1.
Áp dụng công thức, ta được: y - 3 = 1(x - 2), hay y = x + 1.
Các bài toán ứng dụng thường yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các vấn đề thực tế. Để giải các bài toán này, học sinh cần đọc kỹ đề bài, xác định các yếu tố liên quan đến hàm số, và xây dựng phương trình phù hợp.
Bài 16 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt nhất. Chúc các em học tập tốt!