Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 21 trang 109 một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho \(\widehat {CAB} = 30^\circ \). Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh a) MC là tiếp tuyến của đường tròn (O). b) \(MC = R\sqrt 3 \).
Đề bài
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC, sao cho \(\widehat {CAB} = 30^\circ \). Lấy điểm M sao cho B là trung điểm của đoạn thẳng OM. Chứng minh
a) MC là tiếp tuyến của đường tròn (O).
b) \(MC = R\sqrt 3 \).
Phương pháp giải - Xem chi tiết
a) Bước 1: Chứng minh \(CB = OB = BM\).
Bước 2: Dựa vào tính chất: Trong một tam giác, đường trung tuyến ứng với một cạnh và bằng nửa cạnh ấy thì tam giác đó vuông, ta chứng minh được \(CM \bot OC\).
b) Áp dụng tỉ số lượng giác trong tam giác vuông OCM để tính CM.
Lời giải chi tiết
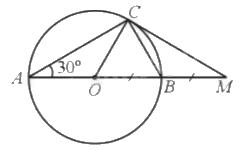
a) Xét tam giác OAC có \(OA = OC\left( { = R} \right)\) nên tam giác OAC cân tại O, do đó \(\widehat A = \widehat {ACO} = 30^\circ \).
Xét tam giác ABC có \(OA = OB = OC = \frac{{AB}}{2}\left( { = R} \right)\) nên tam giác ABC vuông tại C, nên \(\widehat {ACB} = 90^\circ \).
Ta có \(\widehat {ACO} + \widehat {OCB} = \widehat {ACB} = 90^\circ \), suy ra \(\widehat {OCB} = 90^\circ - \widehat {ACO} = 90^\circ - 30^\circ = 60^\circ \).
Xét tam giác OCB có \(OB = OC\left( { = R} \right)\) và \(\widehat {OCB} = 60^\circ \) nên tam giác OCB đều,
do đó \(OC = OB = CB.\)
Vậy \(OC = OB = CB = BM.\)
Xét tam giác OCM có\(MB = OB = CB = \frac{{OM}}{2}\) nên tam giác OCM vuông tại C,
hay \(CM \bot OC\).
Do đó MC là tiếp tuyến của đường tròn (O).
b) Do tam giác OCM vuông tại C và \(\widehat {COB} = 60^\circ \) nên \(\widehat M = 30^\circ \)
Ta có \(\tan M = \frac{{OC}}{{MC}}\) hay \(MC = \frac{{OC}}{{\tan M}} = \frac{R}{{\tan 30^\circ }} = R\sqrt 3 \).
Bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản sau:
Bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1 thường yêu cầu học sinh vận dụng kiến thức về hàm số để giải quyết các bài toán liên quan đến các tình huống thực tế. Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Một người đi xe đạp từ A đến B với vận tốc 12km/h. Hỏi sau bao lâu người đó đến B nếu quãng đường AB dài 36km?)
Giải:
Gọi t là thời gian người đó đi từ A đến B (đơn vị: giờ). Quãng đường AB là 36km, vận tốc của người đó là 12km/h. Ta có công thức:
Quãng đường = Vận tốc × Thời gian
=> 36 = 12 × t
=> t = 36 / 12 = 3 (giờ)
Vậy người đó đi từ A đến B mất 3 giờ.
Ngoài bài 21 trang 109, sách bài tập toán 9 - Cánh diều tập 1 còn có nhiều bài tập tương tự liên quan đến hàm số. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về hàm số và có thể giải quyết các bài tập tương tự một cách hiệu quả, bạn nên luyện tập thêm các bài tập khác trong sách bài tập toán 9 - Cánh diều tập 1 và các tài liệu tham khảo khác. Bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học toán 9 để được hướng dẫn chi tiết hơn.
Bài 21 trang 109 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số và rèn luyện kỹ năng giải toán. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn đã có thể giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!