Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 14 trang 14 một cách cẩn thận, kèm theo các giải thích chi tiết để giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét. a) Viết hệ hai phương trình bậc nhất hai ấn x, y biểu thị m
Đề bài
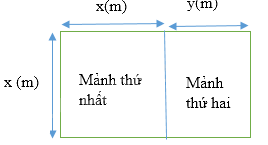
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét.
a) Viết hệ hai phương trình bậc nhất hai ấn x, y biểu thị mối quan hệ giữa các đại lưọng.
b) Cặp số (13 ; 9,6) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
Phương pháp giải - Xem chi tiết
a) Bước 1: Viết phương trình biểu diễn chu vi của cả khu đất.
Bước 2: Viết phương trình biểu diễn chi phí xây tường rào.
b) Thay cặp số (13; 9,6) vào từng phương trình, nếu kết quả của vế trái ở mỗi phương trình bằng vế phải của phương trình đó thì cặp số đó là nghiệm của hệ phương trình.
Lời giải chi tiết
a) Chu vi mảnh đất thứ nhất và mảnh đất thứ 2 lần lượt là \(4x(m)\) và \(2(x + y)(m)\).
Do chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m nên ta có phương trình \(4x - 2(x + y) = 6,8\) hay \(x - y = 3,4\). (1)
Chiều dài cạnh của khu đất là \(x + y(m)\).
Trên cạnh đó, người ta xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét nên ta có phương trình \(50000(x + y) = 1130000\) hay \(x + y = 22,6.\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}x - y = 3,4\\x + y = 22,6\end{array} \right.\)
b) Thay x = 13; y = 9,6 vào từng phương trình \(x - y = 3,4\) trong hệ, ta có:
\(13 - 9,6 = 3,4\) và \(13 + 9,6 = 22,6\)
Vậy hệ phương trình trên nhận cặp số (13; 9,6) làm nghiệm.
Bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về các dạng bài tập liên quan đến hàm số bậc nhất. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1 thường yêu cầu học sinh:
Dưới đây là lời giải chi tiết cho từng phần của bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu, kèm theo các giải thích chi tiết để giúp bạn nắm vững kiến thức.
...
...
...
Để giúp bạn hiểu rõ hơn về cách giải bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1, chúng tôi sẽ cung cấp một số ví dụ minh họa và bài tập tương tự. Bạn có thể tự giải các bài tập này để củng cố kiến thức và kỹ năng của mình.
Ví dụ 1: Cho hàm số y = 2x + 3. Hãy tìm giá trị của y khi x = 1.
Giải: Thay x = 1 vào hàm số y = 2x + 3, ta được y = 2 * 1 + 3 = 5. Vậy, khi x = 1 thì y = 5.
Bài tập 1: Cho hàm số y = -x + 2. Hãy tìm giá trị của x khi y = 0.
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, bạn nên lưu ý những điều sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 14 trang 14 sách bài tập toán 9 - Cánh diều tập 1 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!