Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 32 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để hiểu rõ hơn về cách giải quyết bài toán này nhé!
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = (Rsqrt 3 ) a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB. b) Tính chu vi tam giác MAB. c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất.
Đề bài
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến MA và MB với đường tròn đó (A, B là các tiếp điểm) sao cho MA = \(R\sqrt 3 \)
a) Xác định tâm và bán kính đường tròn nội tiếp tam giác MAB.
b) Tính chu vi tam giác MAB.
c) Vẽ đường thẳng d đi qua M cắt đường tròn (O) tại hai điểm P, Q. Xác định vị trí của đường thẳng d sao cho MQ + MP đạt giá trị nhỏ nhất.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác MAB là tam giác đều suy ra tâm và bán kính đường tròn nội tiếp tam giác MAB.
Sử dụng bất đẳng thức Cosi: a2 + b2\( \ge \) 2ab (Dấu bằng xảy ra khi và chỉ khi a = b).
Lời giải chi tiết
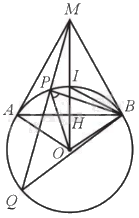
a) Ta có MA, MB là các tiếp tuyến của đường tròn (O) lần lượt tại A và B nên MA ⊥ OA, MB ⊥ OB.
Xét ∆OAM vuông tại A, theo định lí Pythagore, ta có:
\(O{M^2} = M{A^2} + O{A^2} = {\left( {R\sqrt 3 } \right)^2} + {R^2} = 4{R^2}\)
Suy ra OM = 2R.
Gọi I là giao điểm của (O) với tia OM, ta có OI = R nên IM = OM – OI = 2R – R = R.
Do đó, IM = IO = R nên I là trung điểm của OM.
Do ∆OAM vuông tại A nên trung điểm I của cạnh huyền OM là tâm đường tròn ngoại tiếp ∆OAM.
Do ∆OBM vuông tại B nên trung điểm I của cạnh huyền OM là tâm đường tròn ngoại tiếp ∆OBM.
Do đó bốn điểm A, M, B, O cùng nằm trên đường tròn (I) đường kính OM.
Vậy I là tâm đường tròn ngoại tiếp tam giác AMB. (1)
Xét ∆OAM vuông tại A, ta có: \(\sin \widehat {AMO} = \frac{{OA}}{{OM}} = \frac{1}{2}\)
Suy ra \(\widehat {AMO} = {30^o}\).
Do MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M nên MA = MB và MO là tia phân giác của góc AMB, suy ra \(\widehat {AMB} = 2\widehat {AMO} = {2.30^o} = {60^o}\)
Vì vậy tam giác AMB là tam giác đều có MA = MB = AB = \(R\sqrt 3 \) (2)
Từ (1), (2) suy ra đường tròn nội tiếp tam giác đều MAB cạnh \(R\sqrt 3 \)có tâm là I và bán kính là \(\frac{{R\sqrt 3 .\sqrt 3 }}{6} = \frac{R}{2}\).
b) Do tam giác MAB đều cạnh \(R\sqrt 3 \) nên chu vi tam giác MAB bằng \(3R\sqrt 3 \).
c) Ta có \(\widehat {MBO} = \widehat {MBP} + \widehat {PBO} = {90^o}\) suy ra \(\widehat {MBP} = {90^o} - \widehat {PBO}\) (3).
Do ∆OBP cân tại O (do OB = OP) nên ta có:
\(\widehat {PBO} = \widehat {BPO} = \frac{{{{180}^o} - \widehat {BOP}}}{2} = {90^o} - \frac{1}{2}\widehat {BOP}\).
Xét đường tròn (O) có \(\widehat {BQP},\widehat {BOP}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BP nên \(\widehat {BQP} = \frac{1}{2}\widehat {BOP}\).
Do đó \(\widehat {PBO} = {90^o} - \widehat {BQP}\) hay \(\widehat {BQP} = {90^o} - \widehat {PBO}\) (4)
Từ (3) và (4) suy ra \(\widehat {MBP} = \widehat {BQP}\).
Xét ∆MPB và ∆MBQ có:
\(\widehat {MBP} = \widehat {MQB}\)
\(\widehat {BMQ}\) là góc chung
Do đó ∆MPB ᔕ ∆MBQ (g.g).
Suy ra \(\frac{{MB}}{{MQ}} = \frac{{MP}}{{MB}}\) hay MP. MQ = MB2 = \({\left( {R\sqrt 3 } \right)^2} = 3{R^2}\).
Lại có (MQ – MP)2 ≥ 0 hay (MQ + MP)2 ≥ 4MQ.MP
Suy ra (MQ + MP)2 ≥ 4.3R2 = 12R2
Do đó \(MQ + MP \ge \sqrt {12{R^2}} = 2R\sqrt 3 \) (dấu “=” xảy ra khi MQ = MP).
Vậy MQ + MP đạt giá trị nhỏ nhất bằng \(2R\sqrt 3 \), khi đó MP = MQ hay đường thẳng d đi qua M và A hoặc d đi qua M và B.
Bài 32 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét nội dung cụ thể của bài toán. Giả sử bài toán yêu cầu tìm giao điểm của hai đường thẳng hoặc tìm điều kiện để phương trình bậc hai có nghiệm. Dưới đây là một ví dụ minh họa:
Cho hai đường thẳng y = 2x + 1 và y = -x + 4. Tìm tọa độ giao điểm của hai đường thẳng này.
Ngoài việc giải các bài toán cụ thể, học sinh cũng cần luyện tập các dạng bài tập thường gặp để củng cố kiến thức và kỹ năng. Một số dạng bài tập thường gặp bao gồm:
Để học tập môn Toán 9 hiệu quả, học sinh cần:
Bài 32 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán 9.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Là hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hàm số bậc hai | Là hàm số có dạng y = ax2 + bx + c, trong đó a, b và c là các số thực và a ≠ 0. |