Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 11 trang 126 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài tập này một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Các kích thước của hai hình trụ (T) và (T’) (hình trụ (T) ở bên ngoài và hình trụ (T’) ở bên trong) được cho ở Hình 9. a) Viết biểu thức tính thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h. b) Tính chiều cao h, biết a = 16 cm, (b = frac{3}{4}a) và thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3.
Đề bài
Các kích thước của hai hình trụ (T) và (T’) (hình trụ (T) ở bên ngoài và hình trụ (T’) ở bên trong) được cho ở Hình 9.
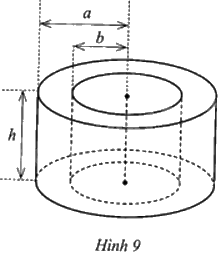
a) Viết biểu thức tính thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h.
b) Tính chiều cao h, biết a = 16 cm, \(b = \frac{3}{4}a\) và thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3.
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích hình trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết
a) Thể tích của hình trụ (T) là: πa2h (cm3).
Thể tích của hình trụ (T’) là: πb2h (cm3).
Thể tích phần ở giữa hai hình trụ (T) và (T’) theo a, b và h là:
πa2h – πb2h = πh(a2 – b2) (cm3).
b) Ta có a = 16 (cm), \(b = \frac{3}{4}a = \frac{3}{4}.16 = 12\) (cm).
Khi đó, thể tích phần ở giữa hai hình trụ (T) và (T') là:
πh.(162 – 122) = 112πh (cm3).
Theo bài, thể tích phần ở giữa hai hình trụ (T) và (T’) là 224π cm3 nên ta có:
112πh = 224π, suy ra h = 2 (cm).
Vậy h = 2 cm.
Bài 11 trang 126 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản sau:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 11 trang 126 thường yêu cầu chúng ta:
(Ở đây sẽ là lời giải chi tiết cho bài 11, bao gồm các bước giải, giải thích và kết luận. Ví dụ, nếu bài toán yêu cầu tìm giao điểm của hai đường thẳng, sẽ trình bày cách lập hệ phương trình và giải hệ đó để tìm tọa độ giao điểm.)
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ xem xét một ví dụ minh họa:
Ví dụ: Cho hàm số y = 2x + 1. Tìm tọa độ giao điểm của đồ thị hàm số với đường thẳng y = -x + 4.
Giải:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Khi giải các bài tập về hàm số, bạn cần lưu ý những điều sau:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 11 trang 126 sách bài tập toán 9 - Cánh diều tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!