Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 107 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho (frac{{MA'}}{{MA}} = frac{{MB'}}{{MB}} = frac{1}{3},frac{{CC'}}{{MC}} = frac{{DD'}}{{MD}} = frac{2}{3},frac{{ME'}}{{E'E}} = frac{1}{2}). Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều.
Đề bài
Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho
\(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{1}{3},\frac{{CC'}}{{MC}} = \frac{{DD'}}{{MD}} = \frac{2}{3},\frac{{ME'}}{{E'E}} = \frac{1}{2}\). Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều.
Phương pháp giải - Xem chi tiết
Dựa vào dữ kiện đề bài và định lí Thalès đảo để chứng minh các góc của ngũ giác A’B’C’D’E’ bằng nhau.
Chứng minh A’B’ = B’C’ = C’D’ = D’E’ = E’A’ rồi suy ra ngũ giác A’B’C’D’E’ là ngũ giác đều.
Lời giải chi tiết
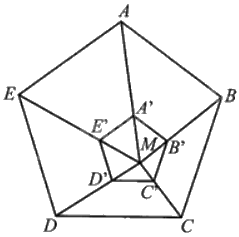
Từ \(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{1}{3},\frac{{CC'}}{{MC}} = \frac{{DD'}}{{MD}} = \frac{2}{3},\frac{{ME'}}{{E'E}} = \frac{1}{2}\) suy ra:
\(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{{MC'}}{{MC}} = \frac{{MD'}}{{MD}} = \frac{{ME'}}{{ME}} = \frac{1}{3}.\) (1)
Do đó: A’B’ // AB, B’C’ // BC, C’D’ // CD, D’E’ // DE, E’A’ // EA (định lí Thalès đảo).
Do A’B’ // AB nên \(\widehat {MA'B'} = \widehat {MAB}\) (đồng vị);
Do E’A’ // EA nên \(\widehat {MA'E'} = \widehat {MAE}\)(đồng vị);
Suy ra \(\widehat {MA'B'} + \widehat {MA'E'} = \widehat {MAB} + \widehat {MAE}\) hay \(\widehat {B'A'E'} = \widehat {BAE}\).
Chứng minh tương tự, ta được các góc A’, B’, C’, D’, E’ của ngũ giác A’B’C’D’E’ tương ứng bằng các góc A, B, C, D, E của ngũ giác đều ABCDE.
Mà ABCDE là ngũ giác đều nên góc A, B, C, D, E của ngũ giác bằng nhau.
Do đó các góc của ngũ giác A’B’C’D’E’ bằng nhau. (2)
Mặt khác, từ (1) ta cũng chứng minh được:
\(A'B' = \frac{{AB}}{3};B'C' = \frac{{BC}}{3};C'D' = \frac{{CD}}{3};\)
\(D'E' = \frac{{DE}}{3};E'A' = \frac{{EA}}{3}\).
Mà ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Do đó: A’B’ = B’C’ = C’D’ = D’E’ = E’A’. (3)
Từ (2) và (3) suy ra ngũ giác A’B’C’D’E’ là ngũ giác đều.
Bài 6 trang 107 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm về hệ số góc, giao điểm của đồ thị hàm số, và các phương pháp giải phương trình bậc hai.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 6 trang 107, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, đây chỉ là một trong nhiều cách giải, bạn có thể tìm tòi và khám phá những phương pháp khác hiệu quả hơn.
Để xác định hệ số góc của đường thẳng, bạn cần đưa phương trình đường thẳng về dạng y = ax + b, trong đó a là hệ số góc. Ví dụ, nếu phương trình đường thẳng là 2x + 3y = 6, bạn cần biến đổi về dạng y = (-2/3)x + 2, suy ra hệ số góc a = -2/3.
Để tìm giao điểm của hai đường thẳng, bạn cần giải hệ phương trình gồm phương trình của hai đường thẳng đó. Ví dụ, nếu hai đường thẳng là y = x + 1 và y = -x + 3, bạn cần giải hệ phương trình:
{ y = x + 1 y = -x + 3 }
Giải hệ phương trình này, ta được x = 1 và y = 2. Vậy giao điểm của hai đường thẳng là (1, 2).
Để giải phương trình bậc hai ax2 + bx + c = 0, bạn có thể sử dụng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a
Trong đó, Δ = b2 - 4ac là biệt thức. Nếu Δ > 0, phương trình có hai nghiệm phân biệt; nếu Δ = 0, phương trình có nghiệm kép; nếu Δ < 0, phương trình vô nghiệm.
Các kiến thức và kỹ năng được học trong bài 6 trang 107 có ứng dụng rộng rãi trong thực tế, chẳng hạn như:
Hy vọng rằng, với lời giải chi tiết và những lời khuyên hữu ích trên đây, bạn đã có thể tự tin giải bài 6 trang 107 sách bài tập toán 9 - Cánh diều tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!