Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 22 trang 131 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 22 trang 131 một cách cẩn thận, kèm theo các giải thích chi tiết để giúp bạn nắm vững kiến thức và kỹ năng giải toán.
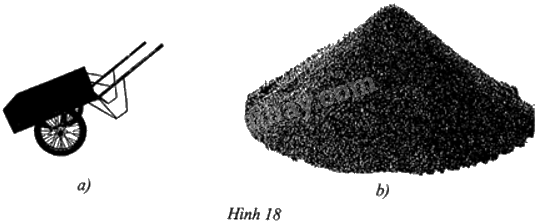
Bác Hà thuê xe cải tiến (Hình 18a) chuyển một đống cát có dạng hình nón với chu vi đáy 9,42 m và chiều cao là 1,2 m (Hình 18b) để xây tường nhà. Biết thùng chứa của xe có dạng hình hộp chữ nhật với kích thước dài 1,57 m, rộng 0,8 m và cao 0,4 m. Trong mỗi chuyến xe, bác Hà chở lượng cát ít hơn thể tích thực của xe là 5%. Hỏi bác Hà cần phải chuẩn bị ít nhất bao nhiêu tiền để chuyển hết đống cát trên, biết rằng giá vận chuyển của một chuyến xe là 90000 đồng?
Đề bài
Bác Hà thuê xe cải tiến (Hình 18a) chuyển một đống cát có dạng hình nón với chu vi đáy 9,42 m và chiều cao là 1,2 m (Hình 18b) để xây tường nhà. Biết thùng chứa của xe có dạng hình hộp chữ nhật với kích thước dài 1,57 m, rộng 0,8 m và cao 0,4 m. Trong mỗi chuyến xe, bác Hà chở lượng cát ít hơn thể tích thực của xe là 5%. Hỏi bác Hà cần phải chuẩn bị ít nhất bao nhiêu tiền để chuyển hết đống cát trên, biết rằng giá vận chuyển của một chuyến xe là 90000 đồng?
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
Gọi bán kính đường tròn đáy của đống cát hình nón đó là r (m) (r > 0).
Do hình nón có chu vi đáy bằng 9,42 m nên ta có 2πr = 9,42 (m).
Suy ra: \(r = \frac{{9,42}}{{2\pi }} \approx 1,5\) (m).
Thể tích đống cát có dạng hình nón là: \(\frac{1}{3}\pi {r^2}h \approx \frac{1}{3}\pi {.1,5^2}.1,2 = 2,826\) (m3).
Thể tích thùng chứa của xe có dạng hình hộp chữ nhật là:
1,57 . 0,8 . 0,4 = 0,5024 (m3).
Mỗi chuyến xe thực chở là:
0,5024.(100% – 5%) = 0,5024 . 95% = 0,47728 (m3).
Ta có: 2,826 : 0,47728 ≈ 5,921.
Vậy để chuyển hết đống cát trên bác Hà cần sử dụng ít nhất 6 chuyến xe và phải dùng số tiền ít nhất là: 6 . 90 000 = 540 000 (đồng).
Bài 22 trang 131 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, đường thẳng song song và vuông góc, và ứng dụng hàm số vào các bài toán hình học.
Bài 22 bao gồm một số câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh khác nhau của hàm số bậc nhất. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản sau:
Dưới đây là hướng dẫn giải chi tiết từng câu hỏi trong bài 22 trang 131 sách bài tập toán 9 - Cánh diều tập 2:
Câu a yêu cầu xác định hệ số góc của đường thẳng y = 2x - 3. Hệ số góc của đường thẳng này là 2.
Câu b yêu cầu xác định tung độ gốc của đường thẳng y = -x + 5. Tung độ gốc của đường thẳng này là 5.
Câu c yêu cầu xác định đường thẳng song song với đường thẳng y = 3x + 1 và đi qua điểm A(1; 2). Đường thẳng song song với y = 3x + 1 có dạng y = 3x + b. Thay tọa độ điểm A(1; 2) vào phương trình, ta có 2 = 3(1) + b, suy ra b = -1. Vậy phương trình đường thẳng cần tìm là y = 3x - 1.
Câu d yêu cầu xác định đường thẳng vuông góc với đường thẳng y = -2x + 4 và đi qua điểm B(0; -1). Đường thẳng vuông góc với y = -2x + 4 có hệ số góc là 1/2. Vậy phương trình đường thẳng cần tìm có dạng y = (1/2)x + b. Thay tọa độ điểm B(0; -1) vào phương trình, ta có -1 = (1/2)(0) + b, suy ra b = -1. Vậy phương trình đường thẳng cần tìm là y = (1/2)x - 1.
Để hiểu rõ hơn về cách giải bài 22, chúng ta hãy xem xét một ví dụ minh họa sau:
Cho hàm số y = (m - 1)x + 2. Tìm giá trị của m để hàm số song song với đường thẳng y = 2x - 1.
Để hàm số y = (m - 1)x + 2 song song với đường thẳng y = 2x - 1, chúng phải có cùng hệ số góc. Do đó, ta có m - 1 = 2, suy ra m = 3.
Để củng cố kiến thức và kỹ năng giải toán, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập toán 9 - Cánh diều tập 2. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên giaitoan.edu.vn.
Bài 22 trang 131 sách bài tập toán 9 - Cánh diều tập 2 là một bài tập quan trọng giúp học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn đã có thể giải quyết bài tập này một cách hiệu quả. Chúc bạn học tốt!