Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 34 trang 116 sách bài tập Toán 9 - Cánh Diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
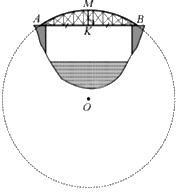
Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40m và chiều cao MK = 6m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).
Đề bài
Một chiếc cầu được thiết kế như một cung AB của đường tròn (O) với độ dài AB = 40m và chiều cao MK = 6m (Hình 35). Tính bán kính của đường tròn chứa cung AMB (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Chứng minh MN là đường trung trực của AB.
Bước 2: Chứng minh \(\Delta AKM\backsim \Delta NKB(g.g)\) để tính NK.
Bước 3: Tính \(MN = 2R = MK + NK\), từ đó suy ra R.
Lời giải chi tiết
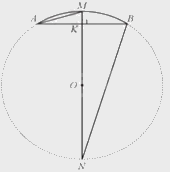
Bài toán được minh họa như hình trên. Kẻ đường kính MN của (O;R), suy ra \(O \in MN\).
Ta có \(AK = KB,MK \bot AB\) nên MK là đường trung trực của AB.
Có \(OA = OB = R\) nên O thuộc đường trung trực của AB.
Suy ra MO hay MN là đường trung trực của AB.
Do K là trung điểm của AN nên \(AK = KB = \frac{{AB}}{2} = \frac{{40}}{2} = 20\)m.
Xét tam giác AKM và tam giác NKB ta có:
\(\widehat {AKM} = \widehat {BKN} = 90^\circ \)
\(\widehat {MAK} = \widehat {MNB}\) (góc nội tiếp cùng chắn cung MB của (O))
Suy ra \(\Delta AKM\backsim \Delta NKB(g.g)\), do đó \(\frac{{AK}}{{NK}} = \frac{{MK}}{{BK}}\), hay \(NK = \frac{{AK.BK}}{{MK}} = \frac{{20.20}}{6} = \frac{{200}}{3}\)m.
Ta có \(MN = 2R = MK + NK = 6 + \frac{{200}}{3} = \frac{{213}}{3}\)m, do đó \(OM = R = \frac{{213}}{3}:2 \approx 36,3\)m.
Vậy bán kính của đường tròn chứa cung AMB khoảng 36,3m.
Bài 34 trang 116 sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến việc xác định hàm số, vẽ đồ thị hàm số và ứng dụng hàm số vào việc giải quyết các bài toán hình học.
Bài 34 bao gồm các dạng bài tập sau:
Đề bài: Xác định hàm số bậc nhất y = ax + b biết rằng đồ thị của hàm số đi qua hai điểm A(0; -2) và B(1; 1).
Lời giải:
Đề bài: Vẽ đồ thị hàm số y = -2x + 3.
Lời giải:
Đề bài: Tìm giao điểm của đồ thị hàm số y = x + 1 và đường thẳng y = -x + 3.
Lời giải:
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
| y = x + 1 | y = -x + 3 | |
|---|---|---|
| Phương trình 1 | y = x + 1 | |
| Phương trình 2 | y = -x + 3 |
Thay y = x + 1 vào phương trình y = -x + 3, ta được: x + 1 = -x + 3 => 2x = 2 => x = 1.
Thay x = 1 vào phương trình y = x + 1, ta được: y = 1 + 1 = 2.
Vậy giao điểm của hai đường thẳng là (1; 2).
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập được trình bày trong bài viết này, bạn đã có thể tự tin giải bài 34 trang 116 sách bài tập Toán 9 - Cánh Diều tập 1 một cách hiệu quả. Chúc bạn học tập tốt!