Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 20 trang 130 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Hình 16 minh hoạ hình nón đỉnh B với đường cao BH và hình nón đỉnh C với đường cao CH có chung đường tròn đáy tâm H. a) Chứng minh rằng: tỉ số thể tích của hình nón đỉnh B và thể tích của hình nón đỉnh C bằng tỉ số đường cao BH và đường cao CH. b) Phát biểu sau đúng hay sai: “Tỉ số thể tích hai hình nón có cùng bán kính đường tròn đáy bằng tỉ số hai đường cao tương ứng của hai hình nón đó”? Vì sao?
Đề bài
Hình 16 minh hoạ hình nón đỉnh B với đường cao BH và hình nón đỉnh C với đường cao CH có chung đường tròn đáy tâm H.
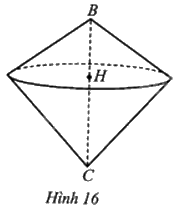
a) Chứng minh rằng: tỉ số thể tích của hình nón đỉnh B và thể tích của hình nón đỉnh C bằng tỉ số đường cao BH và đường cao CH.
b) Phát biểu sau đúng hay sai: “Tỉ số thể tích hai hình nón có cùng bán kính đường tròn đáy bằng tỉ số hai đường cao tương ứng của hai hình nón đó”? Vì sao?
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích của hình nón: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
a) Do hình nón đỉnh B và hình nón đỉnh C có cùng đáy nên ta gọi bán kính đáy của hai hình nón là: r (r > 0).
Thể tích của hình nón đỉnh B là: \(V = \frac{1}{3}\pi {r^2}.BH\).
Thể tích của hình nón đỉnh C là: \(V' = \frac{1}{3}\pi {r^2}.CH\).
Tỉ số thể tích của hình nón đỉnh B và hình nón đỉnh C là: \(\frac{V}{{V'}} = \frac{{\frac{1}{3}\pi {r^2}.BH}}{{\frac{1}{3}\pi {r^2}.CH}} = \frac{{BH}}{{CH}}\)
Vậy tỉ số thể tích của hình nón đỉnh B và thể tích của hình nón đỉnh C bằng tỉ số đường cao BH và đường cao CH.
b) Theo chứng minh ở câu a) ta có phát biểu đã nêu là đúng.
Bài 20 trang 130 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 20 trang 130 sách bài tập toán 9 - Cánh diều tập 2 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 20 trang 130 sách bài tập toán 9 - Cánh diều tập 2, chúng tôi sẽ cung cấp lời giải chi tiết cho từng dạng bài tập.
Để xác định hệ số góc và tung độ gốc của hàm số y = ax + b, bạn cần so sánh hàm số đã cho với dạng tổng quát. Hệ số a là hệ số góc, còn b là tung độ gốc.
Ví dụ: Cho hàm số y = 2x - 3. Xác định hệ số góc và tung độ gốc của hàm số.
Giải: So sánh hàm số y = 2x - 3 với dạng y = ax + b, ta có a = 2 và b = -3. Vậy hệ số góc của hàm số là 2 và tung độ gốc là -3.
Để tìm điểm thuộc đồ thị hàm số y = ax + b, bạn cần thay giá trị x vào hàm số và tính giá trị y tương ứng. Điểm có tọa độ (x; y) sẽ thuộc đồ thị hàm số.
Ví dụ: Cho hàm số y = x + 1. Tìm điểm thuộc đồ thị hàm số khi x = 2.
Giải: Thay x = 2 vào hàm số y = x + 1, ta có y = 2 + 1 = 3. Vậy điểm có tọa độ (2; 3) thuộc đồ thị hàm số.
Để xác định phương trình đường thẳng đi qua hai điểm A(x1; y1) và B(x2; y2), bạn cần thực hiện các bước sau:
Ví dụ: Xác định phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Giải:
Vậy phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4) là y = x + 1.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, bạn có thể luyện tập thêm với các bài tập tương tự trong sách bài tập toán 9 - Cánh diều tập 2. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 20 trang 130 sách bài tập toán 9 - Cánh diều tập 2 là một bài tập quan trọng giúp bạn ôn tập và củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!