Bài 55 trang 124 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để xác định hệ số góc và đường thẳng song song, vuông góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 55 trang 124 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC. a) Chứng minh \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\). b) Lấy điểm M thuộc cung CD. Chứng minh \(AM > CM\)và \(\widehat {COM} = 2\widehat {CAM}\). c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất.
Đề bài
Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC.
a) Chứng minh \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\).
b) Lấy điểm M thuộc cung CD. Chứng minh \(AM > CM\)và \(\widehat {COM} = 2\widehat {CAM}\).
c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất.
Phương pháp giải - Xem chi tiết
a) Bước 1: Tính số đo các cung CB, CA, CD, AD và từ đó tính được số đo các góc ABC, CAB, COD.
Bước 2: Tính góc ACO (tổng 3 góc trong tam giác ACO).
b) Bước 1: So sánh số đo cung AM và CM, từ đó suy ra \(\widehat {ACM} > \widehat {CAM}\).
Bước 2: Dựa vào mỗi quan hệ giữ góc và cạnh đối diện trong tam giác ACM để so sánh AM, CM.
c) Biểu diễn diện tích tam giác MAC: \(S = \frac{1}{2}AC.MN\)
Ta dự đoán diện tích tam giác MAC khi M là điểm chính giữa của cung AC nên ta chứng minh \(MN \le DK\).
Lời giải chi tiết
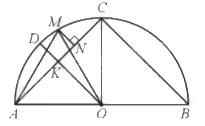
Gọi K là giao điểm của AC và OD, kẻ MN vuông góc với AC tại N.
a) Vì C điểm chính giữa của cung AB nên $\text{sđ}\overset\frown{CB}=\text{sđ}\overset\frown{CA}=\frac{1}{2}\text{sđ}\overset\frown{AB}=\frac{1}{2}.180{}^\circ =90{}^\circ $ (do AB là cung chắn nửa đường tròn nên có số đo là 180⁰),
Suy ra \(\widehat {BAC} = \widehat {ABC} = \frac{{90^\circ }}{2} = 45^\circ \)(do \(\widehat {BAC}\)và \(\widehat {ABC}\)là các góc nội chắn các cung bằng nhau) (1) và \(\widehat {COA} = 90^\circ \)(góc ở tâm chắn cung AC).
Do D là điểm chính giữa của cung AC nên $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}=\frac{1}{2}\text{sđ}\overset\frown{AC}=\frac{1}{2}.90{}^\circ =45{}^\circ $
Suy ra \(\widehat {COD} = 45^\circ \) (do \(\widehat {COD}\) là góc ở tâm chắc cung DC)(2)
Xét tam giác ABC có: \(\widehat {ACO} = 180^\circ - \widehat {CAO} - \widehat {COA} = 180^\circ - 45^\circ - 90^\circ = 45^\circ \) (3)
Từ (1), (2), (3) suy ra \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\left( { = 45^\circ } \right)\).
b) Do M thuộc cung nhỏ DC và $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}=45{}^\circ $, mà $\text{sđ}\overset\frown{AM}=\text{sđ}\overset\frown{AD}\text{+sđ}\overset\frown{DM}=45{}^\circ \text{+sđ}\overset\frown{DM}$
Nên $\text{sđ}\overset\frown{AM}>45{}^\circ $ và $\text{sđ}\overset\frown{CM}<45{}^\circ $, do đó $\text{sđ}\overset\frown{AM}>\text{sđ}\overset\frown{CM}$ hay \(\widehat {ACM} > \widehat {CAM}\)
Xét tam giác ACM có \(\widehat {ACM} > \widehat {CAM}\) nên \(AM > CM\).
Xét (O) có: \(\widehat {CAM}\) là góc nội tiếp chắn cung CM nên $\widehat{CAM}\text{=}\frac{1}{2}\text{sđ}\overset\frown{CM}$; \(\widehat {COM}\) là góc ở tâm chắn cung CM nên $\widehat{COM}\text{=sđ}\overset\frown{CM}$. Do đó \(\widehat {COM} = 2\widehat {CAM}\).
c) Diện tích tam giác MAC là \(S = \frac{1}{2}AC.MN\).
Mà AC cố định nên S lớn nhất khi MN lớn nhất.
Do $\text{sđ}\overset\frown{AD}=\text{sđ}\overset\frown{DC}$ nên \(\widehat {COD} = \widehat {AOD}\) ( do đây là 2 góc ở tâm chắn 2 cung bằng nhau của (O)) nên OD (hay OK) là tia phân giác của góc COA.
Mặt khác \(AO = CO\) (cũng bằng bán kính (O)) nên tam giác ACO cân tại O, do đó đường phân giác OK đồng thời là đường cao, hay \(OK \bot AC\).
Ta lại có \(MN + OK \le OM\)và \(OM = OD = DK + OK\) nên \(MN \le DK\).
Do DK không đổi nên MN lớn nhất khi \(MN = DK\) hay M là điểm chính giữa cung AC.
Vậy diện tích \(\Delta MAC\)lớn nhất bằng \(\frac{1}{2}AC.DK\) khi M là điểm chính giữa cung nhỏ AC.
Bài 55 trang 124 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất để giải quyết các bài toán liên quan đến đường thẳng song song, vuông góc và xác định hệ số góc.
Bài tập yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài 55 trang 124 sách bài tập Toán 9 Cánh diều tập 1, chúng ta cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử chúng ta có đường thẳng y = 2x + 3. Hệ số góc của đường thẳng này là 2. Để tìm một đường thẳng song song với đường thẳng này, chúng ta cần chọn một hệ số góc bằng 2 và một tung độ gốc khác 3. Ví dụ, đường thẳng y = 2x + 5 song song với đường thẳng y = 2x + 3.
Để tìm một đường thẳng vuông góc với đường thẳng y = 2x + 3, chúng ta cần chọn một hệ số góc sao cho tích của nó với 2 bằng -1. Hệ số góc đó là -1/2. Ví dụ, đường thẳng y = -1/2x + 1 vuông góc với đường thẳng y = 2x + 3.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 55 trang 124 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các tính chất của đường thẳng. Bằng cách nắm vững các kiến thức và kỹ năng đã học, các em có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b, a ≠ 0 |
| Hệ số góc | a, xác định độ dốc của đường thẳng |
| Đường thẳng song song | a1 = a2, b1 ≠ b2 |
| Đường thẳng vuông góc | a1 * a2 = -1 |