Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 8 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol (y = - frac{1}{4}{x^2}) trong hệ trục toạ độ Oxy, với gốc toạ độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết kh
Đề bài
Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol \(y = - \frac{1}{4}{x^2}\) trong hệ trục toạ độ Oxy, với gốc toạ độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết khoảng cách giữa điểm A và điểm B là 6 m.

Phương pháp giải - Xem chi tiết
Gọi I là trung điểm của AB.
Bước 1: Tính IA.
Bước 2: Thay tọa độ A hoặc B vào hàm số \(y = - \frac{1}{4}{x^2}\) để tìm h.
Lời giải chi tiết
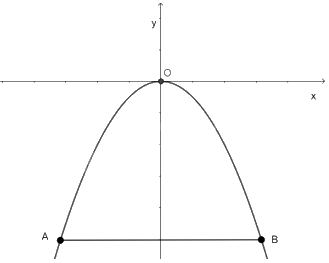
Gọi I là trung điểm của AB, ta có OI là khoảng cách từ O đến AB hay từ O đến mặt nước. Vậy \(h = OI\).
Vì I là trung điểm của AB nên \(AI = BI = \frac{{AB}}{2} = \frac{6}{2} = 3\)cm.
Trong hệ trục tọa độ Oxy có; hoành độ của B là 3, tung độ là \( - h\), và B thuộc đồ thị hàm số \(y = - \frac{1}{4}{x^2}\) nên \( - h = - \frac{1}{4}{.3^2}\), do đó \(h = \frac{9}{4} = 2,25\)m.
Vậy chiều cao h từ điểm O đến mặt nước là 2,25m.
Bài 8 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Bài 8 thường bao gồm các dạng bài tập sau:
Để giải bài 8 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là ví dụ minh họa cách giải một bài tập thuộc dạng 1:
Cho đồ thị của hàm số y = ax + b đi qua hai điểm A(0; 2) và B(1; 4). Hãy xác định hệ số a và b.
Vì đồ thị đi qua điểm A(0; 2), ta có: 2 = a * 0 + b => b = 2.
Vì đồ thị đi qua điểm B(1; 4), ta có: 4 = a * 1 + b => 4 = a + 2 => a = 2.
Vậy, hàm số có dạng y = 2x + 2.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2. Ngoài ra, bạn cũng có thể tham khảo các tài liệu học tập khác hoặc tìm kiếm sự giúp đỡ từ giáo viên và bạn bè.
Bài 8 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.
| Dạng bài | Phương pháp giải |
|---|---|
| Xác định hàm số | Thay tọa độ điểm vào phương trình hàm số |
| Tính giá trị hàm số | Thay giá trị x vào phương trình hàm số |
| Tính chất hàm số | Xác định dấu của hệ số a |