Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 34 trang 72 trong sách bài tập Toán 9 - Cánh Diều tập 2. Chúng tôi cam kết giúp bạn nắm vững kiến thức và tự tin hơn trong việc học tập.
Hàm số nào dưới đây có đồ thị là đường cong ở hình 11: (begin{array}{l}A.y = - sqrt 2 {x^2}\B.y = sqrt 2 {x^2}\C.y = - 2{x^2}\D.y = 2{x^2}end{array})
Đề bài
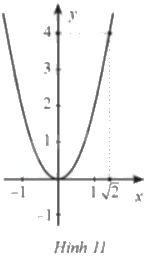
Hàm số nào dưới đây có đồ thị là đường cong ở hình 11:
A. \(y = - \sqrt 2 {x^2}\)
B. \(y = \sqrt 2 {x^2}\)
C. \(y = - 2{x^2}\)
D. \(y = 2{x^2}\)
Phương pháp giải - Xem chi tiết
Ta thấy điểm \(\left( {\sqrt 2 ;4} \right)\) thuộc đồ thị hàm số, vậy tọa độ của nó sẽ thỏa mãn phương trình.
Lời giải chi tiết
Ta thấy điểm \(\left( {\sqrt 2 ;4} \right)\) thuộc đồ thị hàm số.
Với \(x = \sqrt 2 \) ta có: \(2.{\left( {\sqrt 2 } \right)^2} = 4\).
Vậy \(\left( {\sqrt 2 ;4} \right)\) thuộc đồ thị hàm số \(y = 2{x^2}\).
Đáp án D.
Bài 34 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường tập trung vào việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số bậc nhất vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng về hàm số bậc nhất là vô cùng quan trọng để giải quyết thành công bài tập này.
Bài 34 thường bao gồm các dạng bài tập sau:
Để giải bài 34 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Ví dụ: Cho đường thẳng y = 2x - 3. Hãy xác định hệ số góc của đường thẳng này.
Giải: Theo phương trình đường thẳng y = ax + b, hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Hàm số bậc nhất là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán học. Việc học tốt hàm số bậc nhất không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng để học các kiến thức nâng cao hơn trong các lớp học tiếp theo. Ngoài ra, hàm số bậc nhất còn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như kinh tế, kỹ thuật, và khoa học.
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 34 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 một cách hiệu quả. Chúc bạn học tập tốt và đạt được kết quả cao trong môn Toán!