Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 22 trang 91 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O;R). E là điểm tùy ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Đề bài
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O;R). E là điểm tùy ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {BEK} = \widehat {BED} = {45^o}\)suy ra E, K, D thẳng hàng nên khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Lời giải chi tiết
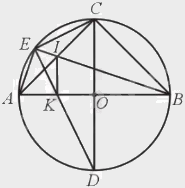
Kẻ đường kính CD suy ra D cố định.
Ta có \(\widehat {AEI} = \widehat {AKI} = {90^o}\) nên tứ giác EIKA nội tiếp đường tròn đường kính AI.
Từ đó suy ra \(\widehat {KAI} = \widehat {KEI}\).
Lại có \(\widehat {KAI} = {45^o}\) (do tam giác ACB vuông cân tại C) do đó \(\widehat {KEI} = {45^o}\) hay \(\widehat {BEK} = {45^o}\) (1).
Mặt khác, \(\widehat {BED} = {45^o}\) (do D là điểm chính giữa của cung AB) (2).
Từ (1) và (2) suy ra E, K, D thẳng hàng.
Vậy khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua điểm D cố định.
Bài 22 trang 91 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài 22 trang 91 Sách bài tập Toán 9 - Cánh Diều tập 2. (Nội dung lời giải chi tiết cho từng câu sẽ được trình bày ở đây, bao gồm các bước giải, giải thích và kết luận.)
Sau khi trình bày lời giải chi tiết, chúng tôi sẽ cung cấp một số ví dụ minh họa và bài tập luyện tập để các em học sinh có thể tự kiểm tra và rèn luyện kỹ năng giải toán. Các bài tập này sẽ được thiết kế với mức độ khó tăng dần, từ dễ đến khó, để phù hợp với trình độ của từng học sinh.
Ngoài ra, chúng tôi cũng sẽ giới thiệu một số kiến thức mở rộng và ứng dụng thực tế của hàm số bậc nhất và hàm số bậc hai trong các lĩnh vực khác nhau của đời sống. Điều này sẽ giúp các em học sinh hiểu rõ hơn về tầm quan trọng và tính ứng dụng của toán học trong thực tế.
Khi giải bài tập về hàm số, các em học sinh cần lưu ý một số điều sau:
Bài 22 trang 91 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trong bài viết này, các em học sinh sẽ tự tin hơn khi giải quyết các bài toán tương tự.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| y = ax2 + bx + c | Hàm số bậc hai |
| x = -b / 2a | Hoành độ đỉnh của parabol |
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!