Bài 33 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 33 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
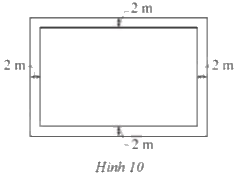
Một mảnh đất hình chữ nhật có chiều rộng x (m), chiều dài gấp rưỡi chiều rộng. Người ta đã làm một vườn hoa ở trung tâm mảnh đất với diện tích bằng 640 m và làm một con đường rộng 2 m xung quanh vườn hoa đó (Hình 10). Hỏi chu vi của mảnh đất đó bằng bao nhiêu mét?
Đề bài
Một mảnh đất hình chữ nhật có chiều rộng x (m), chiều dài gấp rưỡi chiều rộng. Người ta đã làm một vườn hoa ở trung tâm mảnh đất với diện tích bằng 640 m và làm một con đường rộng 2 m xung quanh vườn hoa đó (Hình 10). Hỏi chu vi của mảnh đất đó bằng bao nhiêu mét?
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn chiều dài mảnh đất theo x.
Bước 2: Biểu diễn chiều dài, chiều rộng vườn hoa theo x.
Bước 3: Dựa vào diện tích vườn hoa để lập phương trình.
Bước 4: Giải phương trình, loại giá trị x không phù hợp.
Bước 5: Tìm chiều dài rồi tính chu vi mảnh đất.
Lời giải chi tiết
Chiều dài mảnh đất là \(1,5x\)(m), điều kiện \(x > 0\).
Chiều dài và chiều rộng vườn hoa lần lượt là: \(1,5x - 4\) và \(x - 4\) (m).
Vườn hoa có diện tích là 640m nên ta có
\(\left( {1,5x - 4} \right)\left( {x - 4} \right) = 640\)
hay \(1,5{x^2} - 10x - 624 = 0\)
Ta có \(\Delta ' = {\left( { - 5} \right)^2} - 1,5.\left( { - 624} \right) = 961 > 0\).
Do \(\Delta ' > 0\) nên phương trình có 2 nghiệm phân biệt \(x = \frac{{ - \left( { - 5} \right) - \sqrt {961} }}{{1,5}} = \frac{{ - 52}}{3};x = \frac{{ - \left( { - 5} \right) + \sqrt {961} }}{{1,5}} = 24\)
Ta thấy \(x = 24\) thỏa mãn điều kiện nên chiều rộng mảnh đất là 24m.
Chiều dài mảnh đất là \(1,5x = 1,5.24 = 36\)m.
Chu vi mảnh đất là: \(2\left( {24 + 36} \right) = 120\)m.
Bài 33 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Để giải bài 33 trang 72, chúng ta cần phân tích kỹ đề bài và xác định yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta:
Dưới đây là lời giải chi tiết cho từng phần của bài 33 trang 72:
Để xác định hàm số bậc nhất, chúng ta cần tìm hệ số a và b. Thông thường, đề bài sẽ cung cấp các thông tin như:
Ví dụ, nếu đề bài cho hai điểm A(x1, y1) và B(x2, y2) thuộc đồ thị hàm số y = ax + b, chúng ta có thể sử dụng công thức sau để tìm a và b:
a = (y2 - y1) / (x2 - x1)
b = y1 - ax1
Sau khi xác định được hàm số bậc nhất, chúng ta có thể vẽ đồ thị hàm số bằng cách:
Lưu ý rằng, đồ thị hàm số bậc nhất là một đường thẳng.
Để tìm tọa độ giao điểm của đồ thị hàm số với các đường thẳng khác, chúng ta cần giải hệ phương trình:
{ y = ax + b
y = c (hoặc y = mx + n) }
Nghiệm của hệ phương trình là tọa độ giao điểm của hai đường thẳng.
Các bài toán ứng dụng liên quan đến hàm số bậc nhất thường yêu cầu chúng ta sử dụng hàm số để mô tả mối quan hệ giữa các đại lượng và giải quyết các vấn đề thực tế.
Ví dụ, bài toán có thể yêu cầu chúng ta tính quãng đường đi được của một vật chuyển động đều với vận tốc không đổi, hoặc tính chi phí sản xuất của một sản phẩm dựa trên số lượng sản phẩm được sản xuất.
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em học sinh có thể tham khảo các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2, hoặc tìm kiếm trên các trang web học toán online.
Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin làm bài tập.
Bài 33 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó trong thực tế. Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em học sinh sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán.