Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 15 trang 106 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 15 trang 106 một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (hình 15). Chứng minh EF = ED.
Đề bài
Cho đường tròn tâm O đường kính AB = 2R, bán kính OC vuông góc với AB tại O. Lấy điểm F thuộc đoạn thẳng OB, tia CF cắt đường tròn (O) tại D. Tiếp tuyến tại D của đường tròn (O) cắt AB tại E (hình 15). Chứng minh EF = ED.
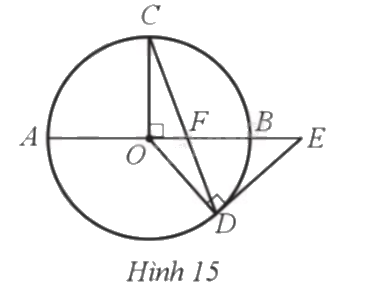
Phương pháp giải - Xem chi tiết
Để chứng minh \(EF = ED\) ta chứng minh như sau:
\(\widehat C + \widehat {OFC} = 90^\circ \),\(\widehat {ODF} + \widehat {FDE} = 90^\circ \) suy ra \(\widehat {FDE} = \widehat {DFE}\) (cùng bằng \(\widehat {OFC}\))
Do đó \(\Delta DEF\) cân tại E suy ra \(EF = ED\)
Lời giải chi tiết
Do DE là tiếp tuyến của (O) nên \(OD \bot DE\) hay \(\widehat {ODE} = 90^\circ \).
Xét tam giác OCD có \(OC = OD( = R)\) nên tam giác OCD cân tại O, do đó \(\widehat C = \widehat {ODF}\).
Ta lại có \(\widehat C + \widehat {OFC} = 90^\circ \)(tam giác OCF vuông tại O), \(\widehat {ODF} + \widehat {FDE} = \widehat {ODE} = 90^\circ \)
Suy ra \(\widehat {OFC} = \widehat {FDE}\), mà \(\widehat {OFC} = \widehat {DFE}\) (đối đỉnh) nên \(\widehat {FDE} = \widehat {DFE}\).
Xét tam giác DFE có \(\widehat {FDE} = \widehat {DFE}\) nên tam giác DFE cân tại E, do đó EF = ED.
Bài 15 trang 106 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số trong các bài toán hình học.
Bài 15 bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 15 trang 106, chúng tôi sẽ cung cấp lời giải chi tiết cho từng câu hỏi:
Đề bài: Xác định hệ số góc của đường thẳng có phương trình y = 2x - 3.
Lời giải: Phương trình đường thẳng có dạng y = ax + b, trong đó a là hệ số góc. Trong phương trình y = 2x - 3, ta có a = 2. Vậy hệ số góc của đường thẳng là 2.
Đề bài: Viết phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc m = -1.
Lời giải: Phương trình đường thẳng có dạng y = mx + b. Thay tọa độ điểm A(1; 2) và hệ số góc m = -1 vào phương trình, ta có: 2 = -1 * 1 + b. Suy ra b = 3. Vậy phương trình đường thẳng là y = -x + 3.
Đề bài: Cho hai điểm B(0; 1) và C(2; 5). Viết phương trình đường thẳng đi qua hai điểm này.
Lời giải: Hệ số góc của đường thẳng đi qua hai điểm B(0; 1) và C(2; 5) là: m = (5 - 1) / (2 - 0) = 2. Phương trình đường thẳng có dạng y = 2x + b. Thay tọa độ điểm B(0; 1) vào phương trình, ta có: 1 = 2 * 0 + b. Suy ra b = 1. Vậy phương trình đường thẳng là y = 2x + 1.
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể áp dụng các mẹo sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 15 trang 106 sách bài tập toán 9 - Cánh diều tập 1 một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!