Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 33 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để hiểu rõ hơn về cách giải quyết bài toán này nhé!
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm độ dài BC để MN có độ dài lớn nhất.
Đề bài
Cho đường tròn (I; r) cố định. Một tam giác ABC thay đổi, có chu vi bằng 16 cm và luôn ngoại tiếp đường tròn (I; r). Một tiếp tuyến song song với BC cắt các cạnh AB, AC lần lượt tại M và N. Tìm dộ dài BC để MN có độ dài lớn nhất.
Phương pháp giải - Xem chi tiết
Sử dụng bất đẳng thức Cosi: a2 + b2\( \ge \) 2ab (Dấu bằng xảy ra khi và chỉ khi a = b).
Lời giải chi tiết
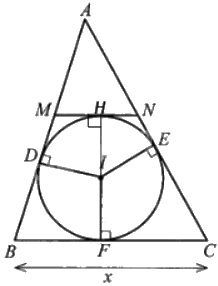
Giả sử đường tròn nội tiếp tam giác ABC tiếp xúc với các cạnh AB, BC, CA lần lượt tại D, F, E và BC = x.
Ta có MN // BC nên ∆AMN ᔕ ∆ABC.
Suy ra: \(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Theo tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN + AM + AN}}{{BC + AB + AC}} = \frac{{chu{\rm{ }}vi\Delta AMN}}{{chu{\rm{ }}vi\Delta ABC}}\) (*)
Vì AD, AE là các tiếp tuyến của đường tròn (I; r) tại D, E nên AD = AE.
Tương tự, ta có BD = BF và CE = CF.
Do đó AD + AE = AB – BD + AC – CE
= AB + AC – (BD + CE)
= AB + AC – (BF + CF)
= AB + AC – BC.
Gọi H là tiếp điểm của đường tròn (I; r) với MN.
Hai tiếp tuyến MD, MH của đường tròn (I; r) cắt nhau tại M nên MD = MH.
Tương tự ta có NE = NH.
Ta có:
Chu vi ∆AMN
= AM + AN + MN
= AD – MD + AE – NE + MN
= AD + AE – (MD + NE) + MN
= AD + AE – (MH + NH) + MN
= AD + AE – MN + MN
= AD + AE
= AB + AC – BC
= AB + AC + BC – 2BC
= Chu vi ∆ABC – 2x (với x = BC)
= 16 – 2x.
Từ (*) ta có: \(\frac{MN}{BC}=\frac{chu\text{ }vi\Delta AMN}{chu\text{ }vi\Delta ABC}\), hay \(\frac{{MN}}{x} = \frac{{16 - 2x}}{{16}}\).
Từ đó MN = \(\frac{{x(16 - 2x)}}{{16}} = \frac{{2x(8 - x)}}{{16}} = \frac{{4x(8 - x)}}{{32}} \le \frac{{{{\left[ {x + (8 - x)} \right]}^2}}}{{32}} = 2\).
Do đó, MN có độ dài lớn nhất bằng 2 cm khi x = 8 – x hay x = 4, tức là BC = 4 cm.
Bài 33 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 33 trang 93, chúng tôi xin trình bày lời giải chi tiết như sau:
Giải thích từng bước, sử dụng công thức và ví dụ minh họa để làm rõ phương pháp giải. Chú trọng việc phân tích đề bài và lựa chọn phương pháp phù hợp.
Tương tự như câu a, giải thích chi tiết từng bước, sử dụng công thức và ví dụ minh họa. So sánh với câu a để làm nổi bật sự khác biệt trong phương pháp giải.
Nếu câu c có nhiều ý nhỏ, chia nhỏ thành các phần và giải thích từng phần. Đảm bảo tính logic và dễ hiểu của bài giải.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tham khảo thêm các bài tập tương tự sau:
Bài 33 trang 93 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng, giúp các em học sinh củng cố kiến thức về hàm số và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng mà chúng tôi đã trình bày, các em sẽ tự tin hơn trong quá trình học tập và làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!