Bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng trong chương trình học toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình thang vuông ABCD (\(\widehat A = \widehat B = 90^\circ \)) với \(\widehat C = 30^\circ \), BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a.
Đề bài
Cho hình thang vuông ABCD (\(\widehat A = \widehat B = 90^\circ \)) với \(\widehat C = 30^\circ \), BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a.
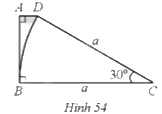
Phương pháp giải - Xem chi tiết
Diện tích của phần tô màu xám = diện tích hình thang ABCD – diện tích quạt tròn CBD.
Bước 1: Áp dụng tỉ số lượng giác để tính DH, CH; từ đó tính được BH.
Bước 2: Chứng minh ABHD là hình chữ nhật, từ đó tính được AB, AD.
Bước 3: Tính diện tích hình thang ABCD, diện tích quạt tròn CBD.
Lời giải chi tiết
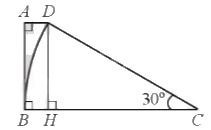
Kẻ \(DH \bot BC\)(\(H \in BC\)) suy ra \(\widehat {CHD} = \widehat {BHD} = 90^\circ \).
Do tam giác CDH vuông tại H nên ta có \(DH = CD.\sin C = a.\sin 30^\circ = a.\frac{1}{2} = \frac{a}{2}\)
và \(CH = CD.\cos C = a.\cos 30^\circ = \frac{{a\sqrt 3 }}{2}\)
Ta có \(BH = BC - CH = a - \frac{{a\sqrt 3 }}{2} = \frac{{a\left( {2 - \sqrt 3 } \right)}}{2}\)
Xét tứ giác ABHD có: \(\widehat A = \widehat B = \widehat {BHD} = 90^\circ \) nên ABHD là hình chữ nhật,
do đó \(AB = DH = \frac{a}{2}\), \(AD = BH = \frac{{a\left( {2 - \sqrt 3 } \right)}}{2}\)
Diện tích hình thang ABCD là
\({S_1} = \frac{{AB\left( {AD + BC} \right)}}{2} = \frac{a}{2}.\left( {\frac{{a\left( {2 - \sqrt 3 } \right)}}{2} + a} \right):2 = \frac{{{a^2}\left( {4 - \sqrt 3 } \right)}}{8}\)
Diện tích quạt tròn BCD là
\({S_2} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi .{a^2}.30}}{{360}} = \frac{{\pi {a^2}}}{{12}}\)
Diện tích phần tô xám là
\(S = {S_1} - {S_2} = \frac{{{a^2}\left( {4 - \sqrt 3 } \right)}}{8} - \frac{{\pi {a^2}}}{{12}} = \frac{{{a^2}\left( {12 - 3\sqrt 3 - 2\pi } \right)}}{{24}}\).
Bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ứng dụng kiến thức về hàm số bậc nhất và hàm số bậc hai vào giải quyết các bài toán thực tế. Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, giaitoan.edu.vn xin trình bày chi tiết lời giải và các bước thực hiện.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 57 thường yêu cầu học sinh:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các công thức sử dụng và các giải thích rõ ràng. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm hàm số bậc nhất đi qua hai điểm A(1; 2) và B(3; 4).
Ngoài bài 57, sách bài tập toán 9 - Cánh diều tập 1 còn nhiều bài tập tương tự về hàm số. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức sau:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp các em học sinh tự tin hơn trong quá trình học tập.
Bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự. Chúc các em học tập tốt!