Bài 10 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
a) Vẽ đồ thị các hàm số (y = - frac{3}{2}{x^2})và (y = frac{3}{2}{x^2})trên cùng một mặt phẳng toạ độ Oxy. b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số (y = - frac{3}{2}{x^2}) và giá trị nhỏ nhất của hàm số (y = frac{3}{2}{x^2}) là bao nhiêu?
Đề bài
a) Vẽ đồ thị các hàm số \(y = - \frac{3}{2}{x^2}\) và \(y = \frac{3}{2}{x^2}\) trên cùng một mặt phẳng toạ độ Oxy.
b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = - \frac{3}{2}{x^2}\) và giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Để vẽ đồ thị hàm số bậc hai ta cần lập bảng giá trị của hàm số đó, cần ít nhất 5 giá trị để để vẽ đồ thị hàm số chuẩn hơn.
- Khi x tăng đồ thị hàm số đi lên tức là giá trị y tăng và ngược lại, do đó ta có thể dự đoán giá trị lớn nhất và giá trị nhỏ nhất
Lời giải chi tiết
a) Lập bảng giá trị của hàm số \(y = - \frac{3}{2}{x^2}\) ta được

Đồ thị hàm số \(y = - \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1; - \frac{3}{2}} \right);\) \(\left( { - 1; - \frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2; - 6} \right);\) \(\left( { - 2; - 6} \right)\)
Lập bảng giá trị của hàm số \(y=\frac{3}{2}{{x}^{2}}\) ta được

Đồ thị hàm số \(y = \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1;\frac{3}{2}} \right);\) \(\left( { - 1;\frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2;6} \right);\) \(\left( { - 2;6} \right)\)
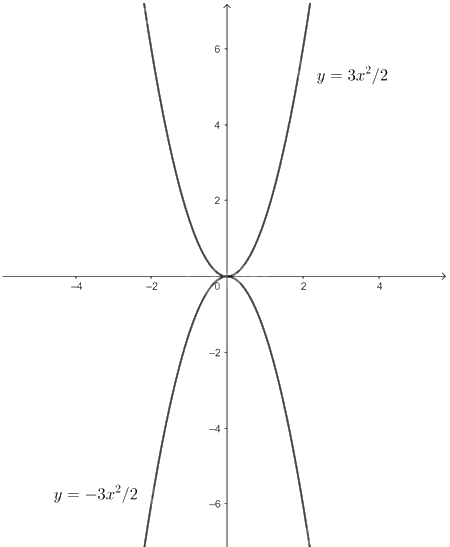
b) Qua đồ thị hàm số ta thấy khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = - \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = - \frac{3}{2}.{\left( {0,5} \right)^2} = - \frac{3}{8}\).
Và khi x tăng từ 0,5 đến 2 thì giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = \frac{3}{2}.{\left( {0,5} \right)^2} = \frac{3}{8}\).
Bài 10 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 10 yêu cầu học sinh giải quyết một bài toán liên quan đến việc xác định hàm số bậc nhất dựa trên các thông tin cho trước. Thông thường, bài toán sẽ cung cấp các điểm mà đồ thị của hàm số đi qua hoặc các thông tin về hệ số góc và giao điểm với trục tung.
Để giải bài 10 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2, học sinh có thể áp dụng các phương pháp sau:
Giả sử bài toán yêu cầu tìm hàm số bậc nhất đi qua hai điểm A(1; 2) và B(-1; 0). Ta thực hiện như sau:
| a | b | |
|---|---|---|
| Phương trình 1 | 1 | 1 |
| Phương trình 2 | -1 | 1 |
Cộng hai phương trình, ta được 2b = 2 => b = 1. Thay b = 1 vào phương trình 1, ta được a + 1 = 2 => a = 1.
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý:
Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2 hoặc trên các trang web học toán online.
Bài 10 trang 58 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất. Bằng cách nắm vững kiến thức và áp dụng đúng phương pháp giải, các em học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự khác.