Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 27 trang 90 trong sách bài tập Toán 9 - Cánh Diều tập 1. Chúng tôi cam kết giúp bạn nắm vững kiến thức và tự tin hơn trong việc học Toán.
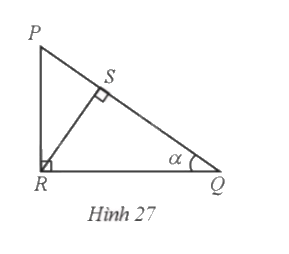
Cho tam giác PQR vuông tại R có đường cao RS và \(\widehat Q = \alpha \) (Hình 27). Ti số lượng giác \(\sin \alpha \) bằng:
Đề bài
Cho tam giác PQR vuông tại R có đường cao RS và \(\widehat Q = \alpha \) (Hình 27). Ti số lượng giác \(\sin \alpha \) bằng:
A. \(\frac{{PR}}{{RS}}\)
B. \(\frac{{PR}}{{QR}}\)
C. \(\frac{{PS}}{{RS}}\)
D. \(\frac{{RS}}{{QR}}\)
Phương pháp giải - Xem chi tiết
Dựa vào tỉ số lượng giác: \(\sin \alpha \) = cạnh đối / cạnh huyền.
Lời giải chi tiết
Do RS là đường cao của tam giác PRQ nên \(\widehat {RSQ} = 90^\circ \).
Xét tam giác RSQ vuông tại S, ta có: \(\sin Q = \sin \alpha = \frac{{RS}}{{RQ}}\).
Đáp án D.
Bài 27 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về xác định hàm số, tính giá trị của hàm số tại một điểm cho trước, và giải các bài toán liên quan đến ứng dụng của hàm số bậc nhất trong thực tế.
Bài 27 thường bao gồm các dạng bài tập sau:
Để giải bài 27 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 1 một cách hiệu quả, bạn cần:
Bài tập: Cho hàm số y = 2x - 1. Tính giá trị của y khi x = 3.
Giải: Thay x = 3 vào hàm số y = 2x - 1, ta được:
y = 2 * 3 - 1 = 6 - 1 = 5
Vậy, khi x = 3 thì y = 5.
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Bài 27 trang 90 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong môn Toán.