Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 3 trang 85 một cách cẩn thận, kèm theo các giải thích chi tiết để bạn có thể nắm vững kiến thức và áp dụng vào các bài tập tương tự.
Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC. a) Chứng minh rằng: - Ba điểm A, O, I cùng thuộc một đường thẳng; - Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC. b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Đề bài
Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC.
a) Chứng minh rằng:
- Ba điểm A, O, I cùng thuộc một đường thẳng;
- Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC.
b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất đường kính và dây cung chứng minh \(OH \bot BC\), \(IH \bot BC\) và \(AH \bot BC\).
Chứng minh \(\Delta \)ACH \(\backsim \)\(\Delta \)ADC suy ra R. Dựa vào tỉ số đồng dạng tìm r.
Lời giải chi tiết
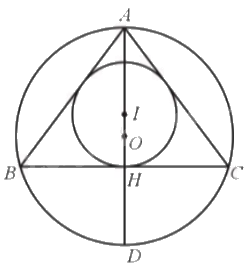
a) Gọi H là chân đường cao hạ từ A.
Tam giác ABC cân tại A, đường cao AH. Suy ra AH là đường trung tuyến của tam giác ABC.
Suy ra BH = HC. Vậy \(OH \bot BC\)(tính chất đường kính và dây cung).
Tương tự, ta có \(IH \bot BC\) mà \(AH \bot BC\)nên A, O, I, H thẳng hàng hay cùng thuộc một đường thẳng.
Ta có A, O, I, H thẳng hàng mà \(OH \bot BC\) nên \(OA \bot BC\). Ta có AD là đường kính của đường tròn (O; OD) nên D cùng nằm trên đường thẳng A, I, O, H suy ra AD là đường trung trực của tam giác ABC. Vậy OA đi qua điểm chính giữa D (khác điểm A) của cung BC.
b) Do BC = 24 cm, AC = 20 cm nên ta có AH = \(\sqrt {A{C^2} - H{C^2}} \) = 16 (cm).
Lại có \(\Delta \)ACH \(\backsim \)\(\Delta \)ADC nên AC2 = AH.AD, suy ra 202 = 16.AD hay AD = 25 cm.
Do đó R = AD : 2 = 12,5 cm.
Do BI là phân giác của góc ABH nên \(\frac{{IH}}{{IA}} = \frac{{BH}}{{BA}} = \frac{{12}}{{20}} = \frac{3}{5}\).
Ta có \(\frac{{IH}}{{IA}} = \frac{3}{5}\) hay \(\frac{{IH}}{{IH + IA}} = \frac{3}{{3 + 5}} = \frac{3}{8}\), tức là \(\frac{r}{{16}} = \frac{3}{8}\). Vì vậy r = 6 cm.
Bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số và cách xác định phương trình đường thẳng.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 3 trang 85, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập:
Để xác định hệ số góc của đường thẳng có phương trình y = ax + b, ta chỉ cần xác định giá trị của a. Hệ số góc a cho biết độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải. Nếu a = 0, đường thẳng là đường thẳng ngang.
Để tìm giao điểm của hai đường thẳng y = a1x + b1 và y = a2x + b2, ta giải hệ phương trình:
| y = a1x + b1 | y = a2x + b2 |
|---|---|
| Giải hệ phương trình để tìm x và y. | Giao điểm của hai đường thẳng là tọa độ (x, y) tìm được. |
Có nhiều cách để lập phương trình đường thẳng:
Trong các bài toán thực tế, hàm số bậc nhất thường được sử dụng để mô tả mối quan hệ giữa hai đại lượng thay đổi. Ví dụ, hàm số có thể mô tả mối quan hệ giữa quãng đường đi được và thời gian, hoặc giữa giá cả và số lượng sản phẩm.
Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn đã có thể tự tin giải bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!