Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 27 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Cho tam giác ABC vuông tại A có đường cao AH = 2,4 cm và (frac{{AB}}{{AC}} = frac{3}{4}). Tính bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R của tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH = 2,4 cm và \(\frac{{AB}}{{AC}} = \frac{3}{4}\). Tính bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R của tam giác ABC.
Phương pháp giải - Xem chi tiết
Dựa vào dữ kiện đề bài để lập các tỉ số rồi tính bán kính đường tròn nội tiếp r và bán kính đường tròn ngoại tiếp R của tam giác ABC.
Lời giải chi tiết
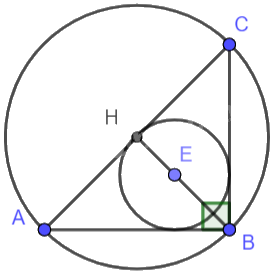
Đặt AB = 3k (k > 0), suy ra AC = 4k (do \(\frac{{AB}}{{AC}} = \frac{3}{4}\)). Lại có tam giác ABC vuông tại A nên BC = 5k. Mặt khác BC.AH = AB. AC nên 5k . AH = 3k. 4k suy ra AH = 2,4k.
Mà AH = 2,4 nên ta có 2,4k = 2,4 suy ra k = 1 nên AB = 3 cm, AC = 4 cm, BC = 5 cm. Mặt khác, do \(r = \frac{{AB + AC - BC}}{2},R = \frac{{BC}}{2}\) suy ra r = 1 cm và R = 2,5 cm.
Bài 27 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số, bao gồm:
Bài 27 thường bao gồm các câu hỏi và bài tập liên quan đến việc xác định hàm số bậc nhất dựa trên các thông tin đã cho. Các bài tập có thể yêu cầu:
Ví dụ: Cho hai điểm A(1; 2) và B(-1; 0). Hãy tìm hàm số y = ax + b đi qua hai điểm này.
Giải:
Ngoài dạng bài tập trên, còn có nhiều dạng bài tập tương tự khác. Để giải quyết các dạng bài tập này, học sinh cần:
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý:
Bài 27 trang 92 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
| Kiến thức cần nắm vững | Phương pháp giải |
|---|---|
| Định nghĩa hàm số bậc nhất | Thay tọa độ điểm vào phương trình hàm số |
| Hệ số a và b | Giải hệ phương trình để tìm a và b |
| Cách xác định hàm số | Kiểm tra lại kết quả |