Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 6 trang 85 một cách cẩn thận, kèm theo các giải thích rõ ràng để giúp bạn nắm vững kiến thức.

Cho tam giác nhọn ABC ((widehat B > widehat C)), phân giác AM. Gọi O, O1, O2 lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng: a) OO1, OO2, O1O2 lần lượt là các đường trung trực của AB, AC, AM; b) Tam giác OO1O2 cân.

Đề bài

Cho tam giác nhọn ABC (\(\widehat B > \widehat C\)), phân giác AM. Gọi O, O₁, O₂ lần lượt là tâm đường tròn ngoại tiếp các tam giác ABC, AMB, AMC. Chứng minh rằng:

a) OO₁, OO₂, O₁O₂ lần lượt là các đường trung trực của AB, AC, AM;

b) Tam giác OO₁O₂ cân.

Phương pháp giải - Xem chi tiết Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 1

Dựa vào khoảng cách từ tâm đến các điểm đường tròn bằng nhau.

Chứng minh \(\widehat {{\rm{O}}{{\rm{O}}_1}{O_2}} = \widehat {{\rm{O}}{{\rm{O}}_2}{O_1}}\) để suy ra tam giác OO₁O₂ cân.

Lời giải chi tiết

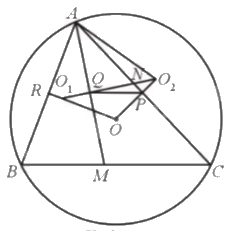
Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 2

a) Do OA = OB và O₁A = O₁B nên OO₁ là đường trung trực của AB.

Tương tự OO₂, O₁O₂ lần lượt là các đường trung trực của AC, AM.

b) Gọi P, Q, R lần lượt là trung điểm của AC, AM, AB; N là giao điểm của QO₂ và AC. Ta có \(\widehat {{\rm{O}}{{\rm{O}}_1}Q} = \widehat {RAQ} = \frac{{\widehat {BAC}}}{2}( = {180^o} - \widehat {R{O_1}Q})\) (1).

Mặt khác \(\widehat {{{\rm{O}}_2}NP} = \widehat {ANQ}\) nên \({90^o} - \widehat {{{\rm{O}}_2}NP} = {90^o} - \widehat {ANQ}\).

Suy ra: \(\widehat {N{O_2}P} = \widehat {QAN} = \frac{{\widehat {BAC}}}{2}\) (2).

Từ (1) và (2) suy ra \(\widehat {{\rm{O}}{{\rm{O}}_1}{O_2}} = \widehat {{\rm{O}}{{\rm{O}}_2}{O_1}}\). Do đó, tam giác OO₁O₂ cân tại O.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 đặc sắc thuộc chuyên mục giải bài tập toán lớp 9 trên nền tảng soạn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2: Tóm tắt lý thuyết và phương pháp giải

Bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản sau:

Hàm số bậc nhất: Dạng y = ax + b (a ≠ 0). Đồ thị là một đường thẳng.
Hàm số bậc hai: Dạng y = ax² + bx + c (a ≠ 0). Đồ thị là một parabol.
Điều kiện để hàm số là bậc nhất/bậc hai: Xác định hệ số a, b, c.
Cách xác định hệ số a, b, c: Sử dụng các điểm thuộc đồ thị hàm số hoặc các thông tin khác được cung cấp trong đề bài.

Giải chi tiết bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2

Để giải bài 6 trang 85, chúng ta cần phân tích kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài toán sẽ yêu cầu chúng ta xác định hàm số, vẽ đồ thị hàm số, hoặc tìm các điểm thuộc đồ thị hàm số. Dưới đây là một ví dụ minh họa cách giải bài toán tương tự:

Ví dụ minh họa

Cho hàm số y = 2x - 3. Hãy xác định hệ số a, b và vẽ đồ thị hàm số.

Xác định hệ số a, b: Trong hàm số y = 2x - 3, ta có a = 2 và b = -3.
Vẽ đồ thị hàm số:
- Chọn hai điểm thuộc đồ thị hàm số. Ví dụ: Khi x = 0, y = -3; Khi x = 1, y = -1.
- Vẽ đường thẳng đi qua hai điểm này.

Các dạng bài tập thường gặp trong bài 6 trang 85

Ngoài việc giải các bài toán cụ thể, bạn cũng cần làm quen với các dạng bài tập thường gặp trong bài 6 trang 85. Một số dạng bài tập phổ biến bao gồm:

Xác định hàm số khi biết các điểm thuộc đồ thị: Sử dụng các điểm đã cho để lập hệ phương trình và giải tìm hệ số a, b, c.
Tìm giao điểm của hai đường thẳng: Giải hệ phương trình hai ẩn để tìm tọa độ giao điểm.
Ứng dụng hàm số vào giải quyết các bài toán thực tế: Ví dụ: Tính quãng đường đi được, tính chi phí, tính lợi nhuận,...

Mẹo giải bài tập hiệu quả

Để giải bài tập toán 9 hiệu quả, bạn có thể áp dụng một số mẹo sau:

Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán trước khi bắt đầu giải.
Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
Sử dụng các công thức và định lý: Áp dụng các công thức và định lý đã học để giải quyết bài toán.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Luyện tập thêm

Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong kỳ thi.

Kết luận

Bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2 là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải toán về hàm số. Hy vọng với những hướng dẫn chi tiết và các mẹo giải bài tập trên, bạn sẽ giải quyết bài toán này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!