Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 11 trang 86 sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để đạt kết quả tốt nhất!
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC của đường tròn đó. Gọi F là giao điểm của EB và CO, I là tâm đường tròn ngoại tiếp tam giác ECF. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì I luôn di chuyển trên một đoạn thẳng cố định.
Đề bài
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O; R). E là điểm tuỳ ý trên cung nhỏ AC của đường tròn đó. Gọi F là giao điểm của EB và CO, I là tâm đường tròn ngoại tiếp tam giác ECF. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì I luôn di chuyển trên một đoạn thẳng cố định.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {CEB} = \widehat {CAB} = {45^o}\). Sau đó chứng minh tam giác ICF vuông cân tại I để suy ra I nằm trên AC.
Lời giải chi tiết
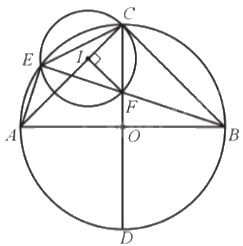
Ta có \(\widehat {CEB} = \widehat {CAB} = {45^o}\)(hai góc nội tiếp cùng chắn cung CB của đường tròn (O)). Mặt khác, I là tâm đường tròn ngoại tiếp tam giác ECF, do đó \(\widehat {CIF} = 2.\widehat {CEF} = {90^o}\). Mà IC = IF suy ra tam giác ICF vuông cân tại I, do đó \(\widehat {ICF} = {45^o}\). Lại có \(\widehat {ACO} = {45^o}\), suy ra I nằm trên AC. Vậy khi E di chuyển trên đoạn thẳng AC cố định.
Bài 11 trang 86 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như các tính chất của hàm số.
Bài 11 yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Hàm số có dạng y = ax + b. Để xác định hệ số góc a và tung độ gốc b, ta cần phân tích biểu thức của hàm số. Ví dụ, nếu hàm số là y = 2x - 3, thì hệ số góc a = 2 và tung độ gốc b = -3.
Để vẽ đồ thị hàm số, ta cần xác định ít nhất hai điểm thuộc đồ thị. Ta có thể chọn hai giá trị tùy ý của x, thay vào phương trình hàm số để tìm giá trị tương ứng của y. Sau đó, vẽ hai điểm này lên hệ trục tọa độ và nối chúng lại bằng một đường thẳng. Đường thẳng này chính là đồ thị của hàm số.
Để tìm tọa độ giao điểm của đồ thị hàm số với trục Ox, ta cho y = 0 và giải phương trình để tìm x. Tọa độ giao điểm là (x, 0). Tương tự, để tìm tọa độ giao điểm của đồ thị hàm số với trục Oy, ta cho x = 0 và giải phương trình để tìm y. Tọa độ giao điểm là (0, y).
Xét hàm số y = -x + 2.
Khi giải bài tập về hàm số bậc nhất, các em cần chú ý những điều sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách bài tập Toán 9 - Cánh Diều tập 2. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 11 trang 86 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp các em học sinh hiểu rõ hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.