Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 36 trang 23 trong sách bài tập Toán 9 - Cánh Diều tập 1. Chúng tôi cam kết giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán tương tự.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
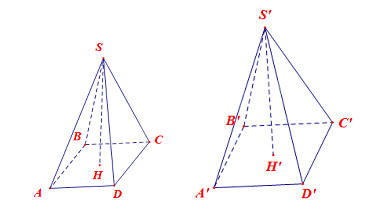
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm.
Đề bài
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm.
Phương pháp giải - Xem chi tiết

Giải hệ gồm 2 phương trình trên ta tìm được độ dài cạnh đáy của mỗi hình chóp.
Lời giải chi tiết
Ta có AB và A’B’ lần lượt là độ dài cạnh đáy của hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’.
Theo đề bài ta có \(A'B' - AB = 2\).
Thể tích hình chóp S.ABCD là \(\frac{1}{3}.A{B^2}.30\) cm3 và hình chóp S’.A’B’C’D’ là \(\frac{1}{3}.A'B{'^2}.30\) cm3.
Do thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3 nên ta có phương trình \(\frac{1}{3}.A'B{'^2}.30 - \frac{1}{3}.A{B^2}.30 = 240\) hay \(A'B{'^2} - A{B^2} = 24\).
Ta lập được hệ phương trình \(\left\{ \begin{array}{l}A'B' - AB = 2\left( 1 \right)\\A'B{'^2} - A{B^2} = 24\left( 2 \right)\end{array} \right.\)
Từ (1) suy ra \(A'B' = 2 + AB\) (3). Thế (3) vào (2) ta được:
\(\begin{array}{l}{\left( {2 + AB} \right)^2} - A{B^2} = 24\\4 + 4AB + A{B^2} - A{B^2} - 24 = 0\\4AB = 20\\AB = 5\end{array}\)
Thay \(AB = 5\) vào (1) ta có \(A'B' = 2 + 5 = 7\).
Vậy độ dài cạnh đáy của 2 hình chóp S.ABCD và S’.A’B’C’D’ lần lượt là 5cm và 7cm.
Bài 36 trang 23 Sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hàm số và tính giá trị của hàm số tại một điểm cho trước. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Bài 36 trang 23 Sách bài tập Toán 9 - Cánh Diều tập 1 thường bao gồm các dạng bài sau:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, học sinh cần:
Bài tập: Cho hàm số y = 2x - 1. Tính giá trị của y khi x = 3.
Giải: Thay x = 3 vào hàm số y = 2x - 1, ta được:
y = 2 * 3 - 1 = 6 - 1 = 5
Vậy, khi x = 3 thì y = 5.
Khi giải bài tập về hàm số bậc nhất, học sinh cần chú ý:
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể tự giải các bài tập sau:
Bài 36 trang 23 Sách bài tập Toán 9 - Cánh Diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng, với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.