Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 30 trang 135 sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 30 trang 135 một cách cẩn thận, kèm theo các giải thích chi tiết để giúp bạn nắm vững kiến thức.
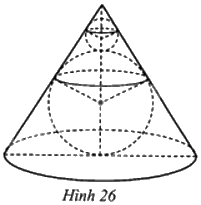
Một món đồ chơi có dạng như Hình 26. Vỏ ngoài món đồ chơi là một hình nón (bằng nhựa trong suốt) có bán kính đường tròn đáy là (3sqrt 3 )cm và đường sinh là (6sqrt 3 )cm. Trong hình nón là hai quả cầu (bằng thuỷ tinh) to và nhỏ, bán kính của chúng lần lượt là 3 cm và 1 cm. Tính tỉ số tổng thể tích của hai quả cầu và thể tích hình nón đó.
Đề bài
Một món đồ chơi có dạng như Hình 26. Vỏ ngoài món đồ chơi là một hình nón (bằng nhựa trong suốt) có bán kính đường tròn đáy là \(3\sqrt 3 \)cm và đường sinh là \(6\sqrt 3 \)cm. Trong hình nón là hai quả cầu (bằng thuỷ tinh) to và nhỏ, bán kính của chúng lần lượt là 3 cm và 1 cm. Tính tỉ số tổng thể tích của hai quả cầu và thể tích hình nón đó.
Phương pháp giải - Xem chi tiết
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Lời giải chi tiết
Tổng thể tích của hai quả cầu là:
\(\frac{4}{3}\pi {.1^3} + \frac{4}{3}\pi {.3^3} = \frac{{112\pi }}{3}\) (cm3).
Ta có công thức tính độ dài đường sinh l qua chiều cao h và bán kính đáy r của hình nón là:
l2 = h2 + r2. Suy ra h2 = l2 – r2.
Khi đó, chiều cao của hình nón là:
\(\sqrt {{{\left( {6\sqrt 3 } \right)}^2} - {{\left( {3\sqrt 3 } \right)}^2}} = \sqrt {81} = 9\) (cm).
Thể tích hình nón là:
\(\frac{1}{3}.\pi .{\left( {3\sqrt 3 } \right)^2}.9 = 81\pi \) (cm3).
Tỉ số tổng thể tích của hai quả cầu và thể tích hình nón là:
\(\frac{{112\pi }}{3}:81\pi = \frac{{112}}{{243}}\)
Bài 30 trang 135 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số.
Bài 30 bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 30 trang 135, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập.
Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải:
Hàm số y = 2x - 3 là hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
So sánh với hàm số đã cho, ta có a = 2 và b = -3.
Vậy, hệ số góc của hàm số là 2 và tung độ gốc là -3.
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Lời giải:
Để tìm tọa độ giao điểm của hai đường thẳng, ta giải hệ phương trình sau:
y = x + 1
y = -x + 3
Thay y = x + 1 vào phương trình y = -x + 3, ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 1, ta được:
y = 1 + 1 = 2
Vậy, tọa độ giao điểm của hai đường thẳng là (1; 2).
Ví dụ: Một người đi xe máy với vận tốc 40 km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Lời giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km).
Ta có hàm số y = 40x.
Khi x = 2, ta có y = 40 * 2 = 80.
Vậy, sau 2 giờ người đó đi được 80 km.
Bài 30 trang 135 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!