Bài 22 trang 88 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 22 trang 88 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
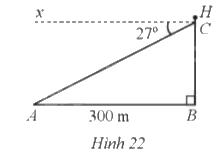
Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB//Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.
Đề bài
Trên mặt biển, khi khoảng cách từ ca nô đến chân tháp hải đăng là AB = 300 m, một người đứng trên tháp hải đăng đó, đặt mắt tại vị trí C và nhìn về phía ca nô theo phương CA tạo với phương nằm ngang Cx một góc là \(\widehat {ACx} = 27^\circ \) (minh hoạ ở Hình 22). Tính chiều cao BH của tháp hải đăng (làm tròn kết quả đến hàng phần trăm của mét), biết AB//Cx và độ cao từ tầm mắt của người đó đến đỉnh tháp hải đăng là CH = 2,1 m.
Phương pháp giải - Xem chi tiết
Bước 1: Tính BC (dựa vào tỉ số lượng giác trong tam giác ABC).
Bước 2: \(BH = BC + CH\).
Lời giải chi tiết
Do AB//Cx nên \(\widehat {BAC} = \widehat {ACx} = 27^\circ \) (so le trong).
Ta lại có tam giác ABC vuông tại C nên \(\tan A = \frac{{BC}}{{AB}}\) hay \(BC = AB.\tan A = 300.\tan 27^\circ \).
Chiều cao BH của tháp hải đăng là:
\(BH = BC + CH = 300.\tan 27^\circ + 2,1 \approx 154,96\)m.
Trước khi đi vào giải chi tiết bài 22 trang 88, chúng ta cùng ôn lại một số kiến thức cơ bản về hàm số bậc nhất và cách giải các bài toán liên quan.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. 'a' được gọi là hệ số góc, quyết định độ dốc của đường thẳng. 'b' là tung độ gốc, là giao điểm của đường thẳng với trục Oy.
Để xác định hệ số góc 'a' và tung độ gốc 'b' của hàm số y = ax + b, ta có thể sử dụng các phương pháp sau:
Để vẽ đồ thị hàm số y = ax + b, ta thực hiện các bước sau:
Đề bài: (Nội dung đề bài cụ thể sẽ được thêm vào đây, ví dụ: Cho hàm số y = 2x - 3. Tìm tọa độ giao điểm của đồ thị hàm số với trục Ox và Oy.)
Lời giải:
Để tìm giao điểm của đồ thị hàm số với trục Ox, ta cho y = 0 và giải phương trình:
0 = 2x - 3
=> 2x = 3
=> x = 3/2
Vậy giao điểm của đồ thị hàm số với trục Ox là A(3/2; 0).
Để tìm giao điểm của đồ thị hàm số với trục Oy, ta cho x = 0 và tính giá trị của y:
y = 2(0) - 3
=> y = -3
Vậy giao điểm của đồ thị hàm số với trục Oy là B(0; -3).
Vậy tọa độ giao điểm của đồ thị hàm số y = 2x - 3 với trục Ox là A(3/2; 0) và với trục Oy là B(0; -3).
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài 22 trang 88 sách bài tập Toán 9 - Cánh diều tập 1 và tự tin giải các bài tập tương tự. Chúc các em học tốt!
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hệ số góc và tung độ gốc | Sử dụng hai điểm thuộc đồ thị hoặc thông tin về giao điểm với trục tọa độ |
| Vẽ đồ thị hàm số | Xác định hai điểm và vẽ đường thẳng |
| Tìm tọa độ giao điểm | Giải hệ phương trình |