Bài 37 trang 73 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học Toán 9. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 37 trang 73 Sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
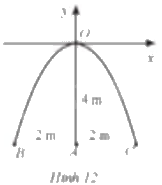
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng (y = a{x^2}), gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
Đề bài
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng \(y = a{x^2}\), gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
Phương pháp giải - Xem chi tiết
Bước 1: Tìm a (dựa vào điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số).
Bước 2: Ta thấy chiều ngang p là \(p = \left| {2x} \right|\) và khoảng cách từ nóc xe đến điểm cao nhất của cổng là 1m nên \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\). Từ đó tìm được p.
Lời giải chi tiết
Dựa vào đồ thị ta thấy: Điểm \(C\left( {2; - 4} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có \( - 4 = a{.2^2}\)
Hay \(a = - 1\). Suy ra hàm số có dạng \(y = - {x^2}\).
Gọi \(K\left( {0; - 1} \right)\) là điểm thuộc Oy. Để xe tải có chiều cao 3 m có chiều ngang p (tức là \(p = \left| {2x} \right|\)) đi vào chính giữa cổng mà không chạm vào cổng thì \(\left| { - {{\left( {\frac{p}{2}} \right)}^2}} \right| < 1\) hay \({p^2} < 4\).
Từ đó suy ra \( - 2 < p < 2\).
Vậy \( - 2 < p < 2\) là giá trị cần tìm.
Bài 37 trang 73 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất và hàm số bậc hai. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Để giải bài 37 trang 73 Sách bài tập Toán 9 - Cánh Diều tập 2, chúng ta cần phân tích đề bài và xác định yêu cầu của bài toán. Sau đó, chúng ta sẽ áp dụng các kiến thức và phương pháp giải đã học để tìm ra đáp án chính xác.
(Nội dung bài giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Bài giải sẽ được chia thành các phần nhỏ để dễ theo dõi và hiểu.)
Ví dụ, nếu bài toán yêu cầu tìm giao điểm của hai đường thẳng, chúng ta sẽ sử dụng phương pháp giải hệ phương trình để tìm tọa độ giao điểm. Nếu bài toán yêu cầu tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số, chúng ta sẽ sử dụng phương pháp tìm đỉnh của parabol.
Ngoài bài 37 trang 73, Sách bài tập Toán 9 - Cánh Diều tập 2 còn có nhiều bài tập tương tự khác. Để chuẩn bị tốt cho các kỳ thi, học sinh nên luyện tập thêm các bài tập sau:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức và phương pháp giải đã học, đồng thời luyện tập thường xuyên để nâng cao kỹ năng giải toán.
Để học tập môn Toán 9 hiệu quả, học sinh nên:
Bài 37 trang 73 Sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán 9.