Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài 32 trang 115 Sách bài tập Toán 9 - Cánh Diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
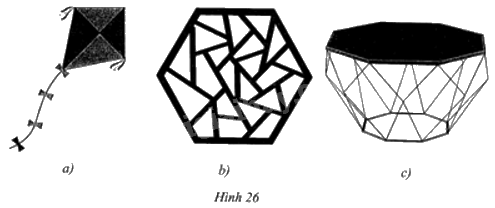
Quan sát bề mặt của chiếc diều, khung cửa sổ, chiếc bàn như ở các hình 26a, 26b, 26c. Các bề mặt của mỗi vật thể đó có dạng hình đa giác đều hay không?
Đề bài
Quan sát bề mặt của chiếc diều, khung cửa sổ, chiếc bàn như ở các hình 26a, 26b, 26c. Các bề mặt của mỗi vật thể đó có dạng hình đa giác đều hay không?
Phương pháp giải - Xem chi tiết
Dựa vào đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
a) Mặt cánh diều không có dạng đa giác đều.
b) Mặt cửa sổ có dạng lục giác đều.
c) Mặt bàn có dạng đa giác đều tám cạnh.
Bài 32 trang 115 Sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, biểu đồ hàm số và ứng dụng của hàm số trong đời sống.
Bài 32 bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 32, chúng tôi sẽ trình bày lời giải chi tiết cho từng dạng bài tập:
Ví dụ: Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải:
Hàm số y = 2x - 3 là hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
So sánh với hàm số đã cho, ta có a = 2 và b = -3.
Vậy, hệ số góc của hàm số là 2 và tung độ gốc là -3.
Ví dụ: Vẽ đồ thị hàm số y = x + 1.
Lời giải:
Để vẽ đồ thị hàm số y = x + 1, ta cần xác định hai điểm thuộc đồ thị. Ta có thể chọn x = 0 và x = -1.
Khi x = 0, y = 0 + 1 = 1. Vậy, điểm A(0; 1) thuộc đồ thị.
Khi x = -1, y = -1 + 1 = 0. Vậy, điểm B(-1; 0) thuộc đồ thị.
Vẽ đường thẳng đi qua hai điểm A(0; 1) và B(-1; 0), ta được đồ thị hàm số y = x + 1.
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.
Lời giải:
Để tìm tọa độ giao điểm của hai đường thẳng, ta cần giải hệ phương trình:
{ y = 2x + 1y = -x + 4 }
Thay y = 2x + 1 vào phương trình y = -x + 4, ta được:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2(1) + 1 = 3
Vậy, tọa độ giao điểm của hai đường thẳng là (1; 3).
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Lời giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km).
Ta có hàm số y = 15x.
Khi x = 2, y = 15(2) = 30.
Vậy, sau 2 giờ người đó đi được 30 km.
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, bạn đã có thể tự tin giải bài 32 trang 115 Sách bài tập Toán 9 - Cánh Diều tập 2. Chúc bạn học tập tốt!