Bài 25 trang 114 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 25 trang 114 sách bài tập Toán 9 - Cánh Diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
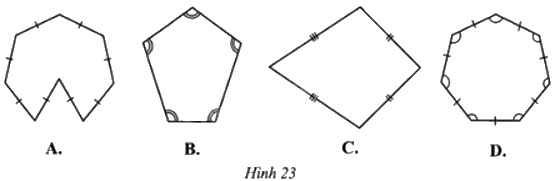
Quan sát các đa giác ở Hình 23 và cho biết hình nào là đa giác đều.
Đề bài
Quan sát các đa giác ở Hình 23 và cho biết hình nào là đa giác đều.
Phương pháp giải - Xem chi tiết
Dựa vào: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
Lời giải chi tiết
Hình A không phải đa giác lồi nên cũng không phải đa giác đều.
Hình B có các cạnh của đa giác không bằng nhau nên không phải đa giác đều.
Hình C có các góc của đa giác không bằng nhau nên không phải đa giác đều.
Hình D là đa giác lồi có các cạnh bằng nhau và các góc bằng nhau nên là đa giác đều.
Bài 25 trang 114 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, đường thẳng song song, vuông góc và ứng dụng vào giải quyết các bài toán liên quan đến thực tế.
Bài tập 25 thường bao gồm các dạng bài sau:
Để giải bài tập 25 trang 114 hiệu quả, học sinh cần nắm vững các kiến thức sau:
Bài 25: Cho đường thẳng y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của đường thẳng này.
Lời giải:
So sánh đường thẳng y = 2x - 3 với dạng tổng quát y = ax + b, ta có:
Vậy, hệ số góc của đường thẳng là 2 và tung độ gốc là -3.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Khi giải bài tập về hàm số bậc nhất, các em cần chú ý:
Bài 25 trang 114 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.