Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 5 trang 107 sách bài tập toán 9 - Cánh diều tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho ngũ giác ABCDE. Chứng minh: AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Đề bài
Cho ngũ giác ABCDE. Chứng minh:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Phương pháp giải - Xem chi tiết
Áp dụng bất đẳng thức trong tam giác là một định lý phát biểu rằng trong một tam giác, chiều dài của một cạnh phải nhỏ hơn tổng, nhưng lớn hơn hiệu của hai cạnh còn lại.
Lời giải chi tiết
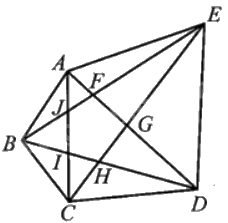
AF + FE > AE (trong tam giác AEF);
AJ + JB > AB (trong tam giác ABJ);
BI + IC > BC (trong tam giác BCI);
CH + HD > CD (trong tam giác CDH);
GE + GD > ED (trong tam giác GDE).
Do đó, ta có:
AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD > AE + AB + BC + CD + ED. (1)
Mặt khác:
(AF + GD) + (JB + FE) + (AJ + IC) + (BI + HD) + (EG + CH) < AD + BE + AC + BD + EC.
Hay AF + FE + AJ + JB + BI + IC + CH + HD + GE + GD < AB + BC + CD + DE + EA. (2)
Từ (1) và (2) suy ra:
AC + AD + BD + BE + EC > AB + BC + CD + DE + EA.
Bài 5 trang 107 sách bài tập toán 9 - Cánh diều tập 2 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, đường thẳng song song và vuông góc, và ứng dụng hàm số vào các bài toán hình học.
Bài 5 bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 5 trang 107, chúng tôi sẽ cung cấp lời giải chi tiết cho từng câu hỏi trong bài tập:
Cho đường thẳng d: y = 2x + 3. Xác định hệ số góc của đường thẳng d.
Lời giải:
Hệ số góc của đường thẳng d: y = 2x + 3 là 2.
Cho hai đường thẳng d1: y = -x + 1 và d2: y = x + 2. Xác định xem hai đường thẳng này có song song hay không.
Lời giải:
Hệ số góc của đường thẳng d1 là -1 và hệ số góc của đường thẳng d2 là 1. Vì hai hệ số góc này khác nhau nên hai đường thẳng d1 và d2 không song song.
Cho điểm A(1; 2) và đường thẳng d: y = 3x - 1. Tìm tọa độ điểm B thuộc đường thẳng d sao cho AB vuông góc với d.
Lời giải:
Gọi B(x0; y0) là tọa độ điểm B. Vì B thuộc đường thẳng d nên y0 = 3x0 - 1. Vector AB = (x0 - 1; y0 - 2). Vector chỉ phương của đường thẳng d là (1; 3). Vì AB vuông góc với d nên tích vô hướng của hai vector này bằng 0:
(x0 - 1) * 1 + (y0 - 2) * 3 = 0
Thay y0 = 3x0 - 1 vào phương trình trên, ta được:
(x0 - 1) + (3x0 - 1 - 2) * 3 = 0
x0 - 1 + 9x0 - 9 = 0
10x0 = 10
x0 = 1
y0 = 3 * 1 - 1 = 2
Vậy tọa độ điểm B là (1; 2). (Lưu ý: trong trường hợp này, điểm A trùng với điểm B)
Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập trên, bạn đã có thể tự tin giải bài 5 trang 107 sách bài tập toán 9 - Cánh diều tập 2. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!