Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 20 trang 91 trong sách bài tập Toán 9 - Cánh Diều tập 2. Chúng tôi cam kết giúp bạn nắm vững kiến thức và tự tin hơn trong việc học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn lời giải bài tập một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu. Hãy cùng bắt đầu nhé!
Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn.
Đề bài
Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn.
Phương pháp giải - Xem chi tiết
Giả sử hình thang cân ABCD. Chứng minh các điểm A, B, C, D đều thuộc đường tròn tâm O, bán kính OA suy ra ABCD nội tiếp đường tròn.
Lời giải chi tiết
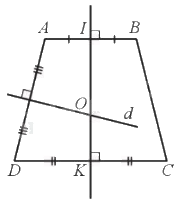
Gọi IK là trục đối xứng của hình thang cân ABCD.
Dựng đường trung trực d của AD.
Gọi O là giao điểm của d và IK.
Dễ thấy OA = OB = OC = OD suy ra các điểm A, B, C, D đều thuộc đường tròn tâm O, bán kính OA hay hình thang cân ABCD nội tiếp đường tròn.
Bài 20 trang 91 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, liên quan đến việc xác định hệ số góc, đường thẳng song song, và ứng dụng hàm số vào các bài toán hình học.
Bài 20 bao gồm các câu hỏi và bài tập nhỏ, tập trung vào các nội dung sau:
Để giải câu a, ta cần xác định hệ số góc của đường thẳng y = 2x - 3. Hệ số góc của đường thẳng này là 2. Sau đó, ta so sánh hệ số góc này với hệ số góc của đường thẳng y = 2x + 1. Vì hai đường thẳng có cùng hệ số góc là 2, nên chúng song song với nhau.
Để giải câu b, ta cần tìm hệ số góc của đường thẳng đi qua hai điểm A(1; 2) và B(3; 6). Hệ số góc của đường thẳng này được tính bằng công thức: (y2 - y1) / (x2 - x1) = (6 - 2) / (3 - 1) = 4 / 2 = 2. Sau đó, ta sử dụng công thức phương trình đường thẳng: y - y1 = m(x - x1) để viết phương trình đường thẳng. Thay các giá trị vào, ta được: y - 2 = 2(x - 1), hay y = 2x.
Để giải câu c, ta cần tìm phương trình đường thẳng song song với đường thẳng y = -x + 5 và đi qua điểm C(2; 1). Vì đường thẳng cần tìm song song với đường thẳng y = -x + 5, nên hệ số góc của nó cũng là -1. Sử dụng công thức phương trình đường thẳng: y - y1 = m(x - x1), ta được: y - 1 = -1(x - 2), hay y = -x + 3.
Kiến thức về hàm số bậc nhất có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kinh tế, kỹ thuật, và khoa học. Ví dụ, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa giá cả và lượng cầu, hoặc để dự đoán sự thay đổi của một đại lượng theo thời gian.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Hy vọng rằng bài giải chi tiết này đã giúp bạn hiểu rõ hơn về cách giải bài 20 trang 91 sách bài tập Toán 9 - Cánh Diều tập 2. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong các kỳ thi.