Bài 15 trang 85 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này thường yêu cầu học sinh xác định hệ số góc, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán liên quan.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 15 trang 85 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại A. Chứng minh \(\tan \frac{{\widehat B}}{2} = \frac{{AC}}{{AB + BC}}\)
Đề bài
Cho tam giác ABC vuông tại A. Chứng minh \(\tan \frac{{\widehat B}}{2} = \frac{{AC}}{{AB + BC}}\)
Phương pháp giải - Xem chi tiết
Bước 1: Kẻ đường phân giác BD.
Bước 2: Áp dụng tỉ số lượng giác trong tam giác vuông ABD: \(\tan {B_1} = \frac{{AD}}{{AB}}\).
Bước 3: Áp dụng tính chất đường phân giác trong tam giác suy ra \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}}\).
Bước 4: Áp dụng tính chất dãy tỉ số bằng nhau:\(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}} = \frac{{AD + CD}}{{AB + BC}} = \frac{{AC}}{{AB + BC}}\)
Lời giải chi tiết
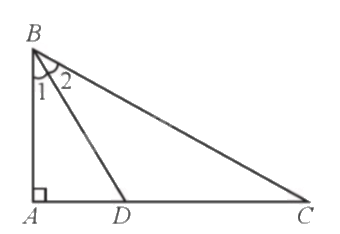
Kẻ đường phân giác BD của tam giác ABC. Khi đó ta có \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{{\widehat B}}{2}\).
Vì tam giác ABD vuông tại A, ta có \(\tan {B_1} = \frac{{AD}}{{AB}}\)(1)
Mà AD là đường phân giác của tam giác ABC nên ta có \(\frac{{AD}}{{CD}} = \frac{{AB}}{{BC}}\), suy ra \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}}\).
Do đó \(\frac{{AD}}{{AB}} = \frac{{CD}}{{BC}} = \frac{{AD + CD}}{{AB + BC}} = \frac{{AC}}{{AB + BC}}\) (2)
Từ (1) và (2) ta có \(\tan {B_1} = \tan \frac{{\widehat B}}{2} = \frac{{AD}}{{AB}} = \frac{{AC}}{{AB + BC}}\).
Bài 15 trang 85 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc nhất. Bài tập này tập trung vào việc vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài 15 trang 85 sách bài tập Toán 9 Cánh diều tập 1 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ:)
Ví dụ: Cho hàm số y = 2x + 1. Hãy xác định hệ số góc của hàm số này.
Giải:
Hàm số y = 2x + 1 là hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Vậy, hệ số góc của hàm số y = 2x + 1 là a = 2.
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý những điều sau:
Để rèn luyện thêm kỹ năng giải bài tập về hàm số bậc nhất, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 15 trang 85 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Tung độ gốc |