Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 21 trang 88 sách bài tập Toán 9 - Cánh Diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
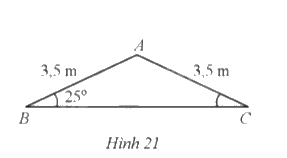
Bạn Hoa vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà và mặt phẳng nằm ngang là \(\widehat {ABC} = 25^\circ \) và độ dài mỗi bên dốc mái là 3,5m (hình 21). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).
Đề bài
Bạn Hoa vẽ mặt cắt đứng phần mái của một ngôi nhà có dạng tam giác cân ABC (mái hai dốc). Biết rằng góc tạo bởi phần mái nhà và mặt phẳng nằm ngang là \(\widehat {ABC} = 25^\circ \) và độ dài mỗi bên dốc mái là 3,5m (hình 21). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết
Bước 1: Kẻ đường cao AH.
Bước 2: Áp dụng tỉ số lượng giác trong tam giác ABH để tình BH.
Bước 3: Tính \(BC = 2BH\).
Lời giải chi tiết
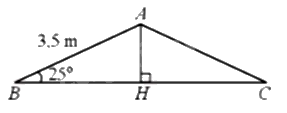
Kẻ đường cao AH của tam giác ABC.
Xét tam giác ABC vuông tại H có \(\cos B = \frac{{BH}}{{BA}}\)
suy ra \(BH = BA.\cos B = 3,5.\cos 25^\circ \).
Do tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến,
do đó \(BC = 2BH = 2.3,5.\cos 25^\circ \approx 6,3\)m.
vậy \(BC \approx 6,3\)m.
Bài 21 trang 88 sách bài tập Toán 9 - Cánh Diều tập 1 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến việc xác định hàm số, vẽ đồ thị hàm số và ứng dụng hàm số vào việc giải quyết các bài toán hình học.
Bài 21 bao gồm các câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để giải bài tập này một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi và bài tập trong bài 21 trang 88 sách bài tập Toán 9 - Cánh Diều tập 1:
Đề bài: Xác định hệ số a của hàm số y = ax + 2 khi đồ thị của hàm số đi qua điểm A(1; 5).
Lời giải: Vì đồ thị của hàm số y = ax + 2 đi qua điểm A(1; 5) nên tọa độ của điểm A thỏa mãn phương trình của hàm số. Thay x = 1 và y = 5 vào phương trình, ta được:
5 = a * 1 + 2
=> a = 5 - 2 = 3
Vậy, hệ số a của hàm số là 3.
Đề bài: Xác định hệ số a của hàm số y = -2x + a khi đồ thị của hàm số đi qua điểm B(-1; 3).
Lời giải: Vì đồ thị của hàm số y = -2x + a đi qua điểm B(-1; 3) nên tọa độ của điểm B thỏa mãn phương trình của hàm số. Thay x = -1 và y = 3 vào phương trình, ta được:
3 = -2 * (-1) + a
=> 3 = 2 + a
=> a = 3 - 2 = 1
Vậy, hệ số a của hàm số là 1.
Đề bài: Xác định hệ số a của hàm số y = ax - 1 khi đồ thị của hàm số đi qua điểm C(2; 1).
Lời giải: Vì đồ thị của hàm số y = ax - 1 đi qua điểm C(2; 1) nên tọa độ của điểm C thỏa mãn phương trình của hàm số. Thay x = 2 và y = 1 vào phương trình, ta được:
1 = a * 2 - 1
=> 2a = 2
=> a = 1
Vậy, hệ số a của hàm số là 1.
Khi giải bài tập về hàm số bậc nhất, bạn cần chú ý:
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, bạn đã có thể hiểu rõ cách giải bài 21 trang 88 sách bài tập Toán 9 - Cánh Diều tập 1. Chúc bạn học tập tốt!