Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 36 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2. Bài viết này sẽ cung cấp phương pháp giải, đáp án chính xác và giải thích rõ ràng từng bước để giúp các em học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài viết này để nắm vững kiến thức và tự tin giải các bài tập Toán 9!
Cho biết đồ thị hàm số (y = left( {m + 2} right){x^2}left( {m ne - 2} right)) đi qua điểm (Aleft( { - 1; - 2} right)). a) Tính giá trị của hàm số tại (x = 3). b) Điểm (Bleft( {0,5; - 0,25} right)) có thuộc đồ thị hàm số hay không? c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó.
Đề bài
Cho biết đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne - 2} \right)\) đi qua điểm \(A\left( { - 1; - 2} \right)\).
a) Tính giá trị của hàm số tại \(x = 3\).
b) Điểm \(B\left( {0,5; - 0,25} \right)\) có thuộc đồ thị hàm số hay không?
c) Tìm một số điểm thuộc đồ thị hàm số (khác điểm O) rồi vẽ đồ thị hàm số đó.
Phương pháp giải - Xem chi tiết
Bước 1: Thay tọa độ điểm A vào hàm số để tìm m, từ đó được công thức cụ thể của hàm số.
a) Bước 2: Thay \(x = 3\) vào hàm số vừa tìm được.
b) Bước 3: Thay hoành độ của B vào vế phải của hàm số rồi so sánh với tung độ của B: nếu giá trị vừa tìm được bằng tung độ của B thì B thuộc đồ thị hàm số và ngược lại.
c) Lấy giá trị x bất kì, từ đó tìm được y tương ứng (lấy ít nhất 4 giá trị).
Lời giải chi tiết
Đồ thị hàm số \(y = \left( {m + 2} \right){x^2}\left( {m \ne - 2} \right)\) đi qua điểm \(A\left( { - 1; - 2} \right)\) nên ta có:
\( - 2 = \left( {m + 2} \right){\left( { - 1} \right)^2}\) hay \( - 2 = m + 2\), suy ra \(m = - 4\) (thỏa mãn điều kiện).
Vậy hàm số có dạng \(y = \left( { - 4 + 2} \right){x^2}\) hay \(y = - 2{x^2}\)
a) Tại \(x = 3\), ta có \(y = - 2{x^2} = - {2.3^2} = - 18\).
Vậy \(x = 3\) thì hàm số có giá trị là \( - 18\).
b) Xét \(B\left( {0,5; - 0,25} \right)\): Với \(x = 0,5\) thì \( - 2{x^2} = - {2.0,5^2} = - 0,5 \ne 0,5\).
Vậy \(B\left( {0,5; - 0,25} \right)\) không thuộc đồ thị hàm số.
c) Bảng giá trị:

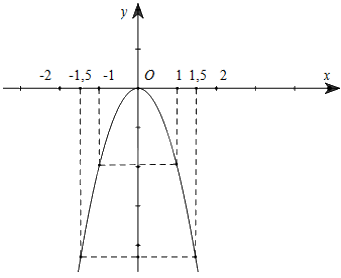
Đồ thị hàm số \(y = - 2{x^2}\) là đường parabol đi qua 5 điểm \(\left( { - 1,5; - 4,5} \right);\left( { - 1; - 2} \right);\left( {0;0} \right);\left( {1; - 2} \right);\left( {1,5; - 4,5} \right)\)
Bài 36 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải các bài toán thực tế, liên quan đến việc xác định hàm số, tìm điểm thuộc đồ thị hàm số và ứng dụng hàm số vào các bài toán hình học.
Bài 36 bao gồm các câu hỏi và bài tập nhỏ, tập trung vào các nội dung sau:
(Giả sử đề bài là: Cho hàm số y = 2x - 3. Tìm tọa độ điểm A thuộc đồ thị hàm số biết A có hoành độ là 1.)
Lời giải:
Vì điểm A thuộc đồ thị hàm số y = 2x - 3 nên ta thay x = 1 vào phương trình hàm số để tìm y:
y = 2 * 1 - 3 = -1
Vậy tọa độ điểm A là (1; -1).
(Giả sử đề bài là: Cho hàm số y = -x + 5. Điểm nào sau đây không thuộc đồ thị hàm số? A(0; 5), B(1; 4), C(-1; 6), D(2; 3))
Lời giải:
Ta thay tọa độ của từng điểm vào phương trình hàm số y = -x + 5 để kiểm tra:
Vậy cả bốn điểm A, B, C, D đều thuộc đồ thị hàm số.
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Để củng cố kiến thức về hàm số bậc nhất, các em có thể tự giải thêm các bài tập sau:
Bài 36 trang 72 sách bài tập Toán 9 - Cánh Diều tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về hàm số bậc nhất và ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập môn Toán 9.