Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 10 trang 15 Sách bài tập Toán 9 - Cánh diều tập 2. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc. Hãy cùng giaitoan.edu.vn khám phá lời giải bài 10 này nhé!
Bảng thống kê kết quả xếp loại học tập Học kì 1 của 500 học sinh khối 9 ở một trường trung học cơ sở như sau (Bảng 18): a) Vẽ biểu đồ đoạn thẳng biểu diễn các dữ liệu thống kê đó. b) Vẽ biểu đồ hình quạt tròn biểu diễn các dữ liệu thống kê đó. c) Tính tỉ số giữa số học sinh xếp loại học tập Tốt và số học sinh xếp loại học tập Khá.
Đề bài
Bảng thống kê kết quả xếp loại học tập Học kì 1 của 500 học sinh khối 9 ở một trường trung học cơ sở như sau (Bảng 18):

a) Vẽ biểu đồ đoạn thẳng biểu diễn các dữ liệu thống kê đó.
b) Vẽ biểu đồ hình quạt tròn biểu diễn các dữ liệu thống kê đó.
c) Tính tỉ số giữa số học sinh xếp loại học tập Tốt và số học sinh xếp loại học tập Khá.
Phương pháp giải - Xem chi tiết
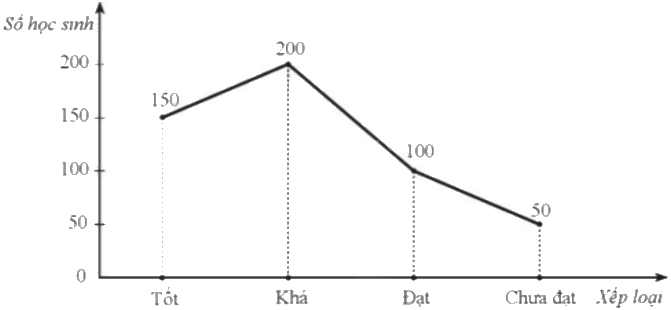
a)Đối tượng thống kê: Trục ngang.
Tiêu chí thống kê: Trục thẳng đứng.
b) Tính tỉ số phần trăm của mỗi đối tượng.
Số đo góc trên biểu đồ của mỗi đối tượng chiếm \(x\% \) là \(x.3,6^\circ \).
c) Tỉ số = (số học sinh xếp loại học tập Tốt) : (số học sinh xếp loại học tập Khá).
Lời giải chi tiết
a) Biểu đồ đoạn thẳng:
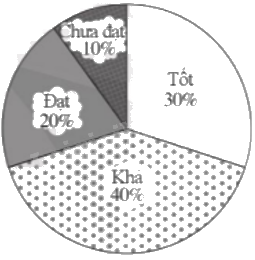
b) Biểu đồ quạt tròn:
Tỉ số phần trăm của số học sinh xếp loại Tốt, Khá, Đạt, Chưa đạt lần lượt là:
\(\frac{{150}}{{500}}.100\% = 30\% ;\frac{{200}}{{500}}.100\% = 40\% ;\frac{{100}}{{500}}.100\% = 20\% ;\frac{{50}}{{500}}.100\% = 10\% ;\)
Số đo các góc trong biểu đồ quạt tròn của số học sinh xếp loại Tốt, Khá, Đạt, Chưa đạt lần lượt là:
\(30.3,6^\circ = 108^\circ ;40.3,6^\circ = 144^\circ ;\\20.3,6^\circ = 72^\circ ;10.3,6^\circ = 36^\circ \).
c) Tỉ số giữa số học sinh xếp loại học tập Tốt và số học sinh xếp loại học tập Khá là: \(\frac{{150}}{{200}} = \frac{3}{4}\)
Bài 10 trang 15 Sách bài tập Toán 9 - Cánh diều tập 2 thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số, và cách xác định phương trình đường thẳng.
Bài 10 bao gồm các câu hỏi nhỏ, yêu cầu học sinh thực hiện các thao tác sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 10, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Hệ số góc của đường thẳng y = 2x - 3 là 2. Hệ số góc này cho biết độ dốc của đường thẳng, tức là khi x tăng lên 1 đơn vị thì y tăng lên 2 đơn vị.
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình sau:
{
Thay phương trình (1) vào phương trình (2), ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình (1), ta được:
y = 1 + 1 = 2
Vậy giao điểm của hai đường thẳng là (1; 2).
Để viết phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4), ta thực hiện các bước sau:
Các kiến thức về hàm số bậc nhất và hàm số bậc hai có ứng dụng rất lớn trong thực tế, như trong việc mô tả các hiện tượng vật lý, kinh tế, và kỹ thuật. Ví dụ, hàm số có thể được sử dụng để mô tả quỹ đạo của một vật thể chuyển động, hoặc để dự đoán doanh thu của một công ty.
Bài 10 trang 15 Sách bài tập Toán 9 - Cánh diều tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và đạt kết quả tốt trong môn Toán.