Bài 21 trang 91 sách bài tập Toán 9 Cánh diều tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 21 trang 91 sách bài tập Toán 9 Cánh diều tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
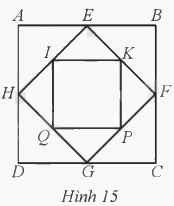
Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo thành tứ giác EFGH, tiếp tục như vậy được tứ giác mới IKPQ (Hình 15). Chứng minh: a) Tứ giác EFGH và tứ giác IKPQ là các tứ giác nội tiếp đường tròn. b) Tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Đề bài
Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo thành tứ giác EFGH, tiếp tục như vậy được tứ giác mới IKPQ (Hình 15). Chứng minh:
a) Tứ giác EFGH và tứ giác IKPQ là các tứ giác nội tiếp đường tròn.
b) Tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Phương pháp giải - Xem chi tiết
Chứng minh tứ giác EFGH và tứ giác IKPQ là hình vuông nên nội tiếp đường tròn.
Dựa vào bán kính đường tròn ngoại tiếp hình vuông là trung điểm của cạnh huyền.
Lời giải chi tiết
a) Do ABCD là hình vuông nên AB = BC = CD = DA và \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\).
Do E, F,G,H lần lượt trung điểm của AB, BC, CD, DA nên AE = EB = BF = FC = CG = GD = DH = HA.
Xét tam giác AHE và tam giác BFE có
\(\widehat A = \widehat B = {90^o}\)
AH = BF
AE = BE
Do đó, \(\Delta AHE = \Delta BFE\) (hai cạnh góc vuông)
Suy ra HE = FE
Tương tự, ta chứng minh được HE = EF = FG =GH.
Khi đó, tứ giác EFGH là hình thoi.
Xét tam giác AHE có \(\widehat A = {90^o}\) và AH = AE nên tam giác AHE vuông cân tại A, suy ra \(\widehat {AEH} = {45^o}\). Tương tự, ta có \(\widehat {BEF} = {45^o}\).
Do đó \(\widehat {HEF} = {180^o} - \widehat {AEH} - \widehat {BEF} = {180^o} - {45^o} - {45^o} = {90^o}\).
Như vậy, hình thoi EFGH là hình vuông. Suy ra EFGH nội tiếp đường tròn.
Chứng minh tương tự ta được tứ giác IKPQ là hình vuông và nội tiếp đường tròn.
b) Xét ∆ABC vuông cân tại B (do và BA = BC) , theo định lí Pythagore, ta có: AC2 = AB2 + BC2 = AB2 + AB2 = 2AB2.
Suy ra AC = AB\(\sqrt 2 \). Bán kính đường tròn ngoại tiếp hình vuông ABCD là: \({R_1} = \frac{{AC}}{2} = \frac{{AB\sqrt 2 }}{2}\).
Tương tự, với ∆AHE vuông cân tại A, ta có: HE = AE\(\sqrt 2 \) = \(\frac{{AB\sqrt 2 }}{2}\).
Với ∆HEF vuông cân tại E, ta có:
\(HF = HE\sqrt 2 = \frac{{AB\sqrt 2 }}{2}.\sqrt 2 = AB\).
Bán kính đường tròn ngoại tiếp hình vuông EFGH là: \({R_2} = \frac{{HF}}{2} = \frac{{AB}}{2}\).
Chứng minh tương tự, ta có bán kính đường tròn ngoại tiếp hình vuông IKPQ là
\({R_3} = \frac{{IP}}{2} = \frac{{IK\sqrt 2 }}{2} = \frac{{IE\sqrt 2 .\sqrt 2 }}{2} = IE = \frac{{HE}}{2} = \frac{{\frac{{AB\sqrt 2 }}{2}}}{2} = \frac{{AB\sqrt 2 }}{4}.\)
Ta có tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH là:
\(\frac{{{R_1}}}{{{R_2}}} = \frac{{\frac{{AB\sqrt 2 }}{2}}}{{\frac{{AB}}{2}}} = \frac{{\sqrt 2 }}{2}.2 = \sqrt 2 \)
Tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ là:
\(\frac{{{R_2}}}{{{R_3}}} = \frac{{\frac{{AB}}{2}}}{{\frac{{AB\sqrt 2 }}{2}}} = \frac{1}{2}.\frac{4}{{\sqrt 2 }} = \sqrt 2 \).
Vậy tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Bài 21 trang 91 sách bài tập Toán 9 Cánh diều tập 2 thuộc chương Hàm số bậc hai. Bài tập này tập trung vào việc xác định hệ số a, b, c của hàm số bậc hai, tìm hoành độ giao điểm của đồ thị hàm số với trục hoành, và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Bài 21 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 21 trang 91 sách bài tập Toán 9 Cánh diều tập 2, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi nhỏ:
Để xác định hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c, các em cần so sánh hàm số đã cho với dạng tổng quát. Ví dụ, nếu hàm số là y = 2x2 - 5x + 3, thì a = 2, b = -5, c = 3.
Delta (Δ) được tính theo công thức Δ = b2 - 4ac. Dựa vào giá trị của Δ, ta có thể xác định số nghiệm của phương trình bậc hai:
Hoành độ giao điểm của đồ thị hàm số với trục hoành là nghiệm của phương trình ax2 + bx + c = 0. Các em có thể sử dụng công thức nghiệm của phương trình bậc hai để tìm ra hoành độ giao điểm.
Xét hàm số y = x2 - 4x + 3. Ta có:
Vậy, đồ thị hàm số y = x2 - 4x + 3 cắt trục hoành tại hai điểm có hoành độ là 1 và 3.
Để giải nhanh các bài tập về hàm số bậc hai, các em nên:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 2 hoặc trên các trang web học toán online.
Bài 21 trang 91 sách bài tập Toán 9 Cánh diều tập 2 là một bài tập quan trọng giúp các em học sinh hiểu sâu hơn về hàm số bậc hai và ứng dụng của nó trong thực tế. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà chúng tôi đã cung cấp, các em sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.