Bài 36 trang 117 sách bài tập Toán 9 Cánh diều tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 36 trang 117 sách bài tập Toán 9 Cánh diều tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho đường tròn (O; 1dm) và ba điểm A, B, C nằm trên đường tròn sao cho \(\widehat {ABC} = 45^\circ \), \(\widehat {ACB} = 15^\circ \). Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) tại E (Hình 36). Tính: a) Số đo cung nhỏ CE và số đo cung lớn BC; b) Độ dài các đoạn thẳng AC, BC.
Đề bài
Cho đường tròn (O; 1dm) và ba điểm A, B, C nằm trên đường tròn sao cho \(\widehat {ABC} = 45^\circ \), \(\widehat {ACB} = 15^\circ \). Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) tại E (Hình 36). Tính:
a) Số đo cung nhỏ CE và số đo cung lớn BC;
b) Độ dài các đoạn thẳng AC, BC.
Phương pháp giải - Xem chi tiết
a) Số đo cung nhỏ CE bằng \(2.\widehat {HAC}\) (do góc HAC nôi tiếp chắc cung nhỏ CE).
Số đo cung lớn BC bằng \(2.\widehat {BAC}\) (do góc BAC nội tiếp chắn cung lớn BC).
b) Bước 1: Chứng minh tam giác OAC vuông cân để tính AC.
Bước 2: Chứng minh \(\Delta OBM = \Delta OCM\) để suy ra \(BM = CM = \frac{{BC}}{2}\)
Bước 3: Tính góc OCM.
Bước 4: Áp dụng tỉ số lượng giác trong tam giác vuông OCM để tính CM.
Bước 5: Tính \(BC = 2CM\).
Lời giải chi tiết
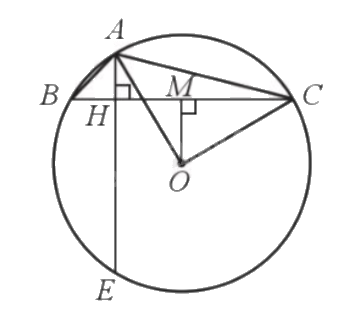
Kẻ OM vuông góc với BC tại M, suy ra \(\widehat {BMO} = \widehat {MCO} = 90^\circ \).
a) Xét tam giác HAC vuông tại H có \(\widehat {HAC} + \widehat {ACH} = 90^\circ \) hay \(\widehat {HAC} = 90^\circ - \widehat {ACH} = 90^\circ - 15^\circ = 75^\circ \)
Mặt khác, \(\widehat {HAC}\) là góc nội tiếp chắn cung nhỏ EC nên số đo cung nhỏ EC là \(2.\widehat {HAC} = 2.75^\circ = 150^\circ \).
Xét tam giác ABC có \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ \) hay
\(\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {ACB}} \right) \\= 180^\circ - \left( {45^\circ - 15^\circ } \right) \\= 120^\circ \)
mà \(\widehat {BAC}\) là góc nội tiếp chắn cung lớn BC nên số đo cung lớn BC là \(2.\widehat {BAC} = 2.120^\circ = 240^\circ \).
b) Ta có góc ABC nội tiếp chắn cung AC của (O), mà \(\widehat {ABC} = 45^\circ \) nên số đo cung AC là \(2.\widehat {ABC} = 2.45^\circ = 90^\circ \).
Do đó góc ở tâm chắn cung AC là góc AOC có số đo bằng \(90^\circ \).
Xét tam giác OAC có \(OA = OC = 1\)dm (cùng bằng bán kính (O)), \(\widehat {AOC} = 90^\circ \) suy ra tam giác OAC vuông cân tại O, do đó \(CA = \sqrt {O{A^2} + O{C^2}} \) (Định lí Pythagore) hay \(CA = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)dm.
Xét 2 tam giác OBM và OCM có
\(OB = OC\) (cùng bằng bán kính (O))
OM chung
\(\widehat {BMO} = \widehat {MCO} = 90^\circ \)
Suy ra \(\Delta OBM = \Delta OCM\) (cạnh huyền – cạnh góc vuông), do đó \(BM = CM = \frac{{BC}}{2}\).
Ta có \(\Delta OAC\) vuông cân nên \(\widehat {OCA} = 45^\circ \). Ta lại có \(\widehat {OCM} = \widehat {OCA} - \widehat {ACB} = 45^\circ - 15^\circ = 30^\circ \)
Mặt khác, tam giác OCM vuông tại M nên \(CM = OC.\cos \widehat {OCM} = 1.\cos 30^\circ = \frac{{\sqrt 3 }}{2}\)dm.
Vậy \(BC = 2CM = 2.\frac{{\sqrt 3 }}{2} = \sqrt 3 \)dm.
Bài 36 trang 117 sách bài tập Toán 9 Cánh diều tập 1 thuộc chương Hàm số bậc hai. Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 36. Ví dụ, nếu bài 36 có 3 câu, sẽ giải thích chi tiết từng câu một. Mỗi câu giải thích rõ ràng các bước thực hiện, công thức sử dụng và kết quả cuối cùng.)
Ví dụ (giả sử bài 36 yêu cầu tìm đỉnh của parabol y = 2x2 - 8x + 5):
Để củng cố kiến thức, bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 9 Cánh diều tập 1. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến hoặc tham gia các khóa học toán online để được hướng dẫn và giải đáp thắc mắc.
Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong việc tính quỹ đạo của vật ném, thiết kế các công trình kiến trúc, và phân tích các hiện tượng kinh tế. Việc nắm vững kiến thức về hàm số bậc hai sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.
Một số bài tập tương tự để luyện tập:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 36 trang 117 sách bài tập Toán 9 Cánh diều tập 1 và tự tin hơn trong việc học tập môn Toán.
| Công thức | Mô tả |
|---|---|
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |
| xI = -b/2a | Hoành độ đỉnh của parabol |
| yI = (4ac - b2)/4a | Tung độ đỉnh của parabol |