Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 13 trang 85 toán 9 - Cánh diều tập 1 một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng.
Tìm x,y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimet).
Đề bài
Tìm x, y trong mỗi hình 14a, 14b, 14c (làm tròn kết quả đến hàng phần mười của centimet).
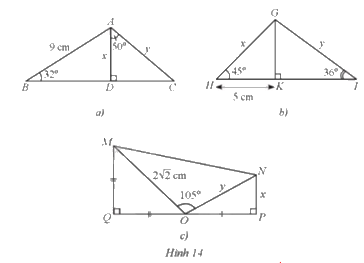
Phương pháp giải - Xem chi tiết
a) Áp dụng tỉ số lượng giác trong tam giác vuông ABD và ADC.
b) Áp dụng tỉ số lượng giác trong tam giác vuông GHK và GHI.
c) Tính QO, OP (dựa vào tam giác vuông cân MQO).
Áp dụng tỉ số lượng giác trong tam giác vuông NOP.
Lời giải chi tiết
a) Xét tam giác ABD vuông tại D, ta có
\(\sin B = \frac{{AD}}{{AB}}\) hay \(\sin 32^\circ = \frac{x}{9}\),
do đó \(x = 9.\sin 32^\circ \approx 4,8\)cm.
Xét tam giác ACD vuông tại D, ta có
\(\cos \widehat {DAC} = \frac{{AD}}{{AC}}\) hay \(\cos 50^\circ = \frac{{4,8}}{y}\),
do đó \(y = \frac{{4,8}}{{\cos 50^\circ }} \approx 7,5\)cm.
b) Xét tam giác GHK vuông tại K, \(\widehat H = 45^\circ \) nên đây là tam giác vuông cân,
suy ra HK = GK = 5cm, và \(\sin I = \frac{{GK}}{{GI}}\) hay \(\sin 36^\circ = \frac{5}{y}\),
do đó \(y = \frac{5}{{\sin 36^\circ }} \approx 8,5\)cm.
c) Xét tam giác MOQ có \(\widehat Q = 90^\circ ,MQ = QO\) nên tam giác MOQ vuông cân tại Q.
Do đó \(M{Q^2} + Q{O^2} = M{O^2}\) hay \(2Q{O^2} = {\left( {2\sqrt 2 } \right)^2}\), nên \(QO = 2\)cm = OP.
Ta lại có tam giác MOQ vuông cân tại Q nên \(\widehat {QOM} = 45^\circ \).
Mặt khác \(\widehat {QOM} + \widehat {MON} + \widehat {NOP} = 45^\circ + 105^\circ + \widehat {NOP} = 180^\circ \), suy ra \(\widehat {NOP} = 30^\circ \)
Xét tam giác vuông NOP có
\(\tan \widehat {NOP} = \frac{{NP}}{{OP}}\) hay \(NP = x = \tan \widehat {NOP}.OP = \tan 30^\circ .2 \approx 1,2\)cm.
Và \(\cos \widehat {NOP} = \frac{{OP}}{{ON}}\) hay \(ON = y = \frac{{OP}}{{\cos \widehat {NOP}}} = \frac{2}{{\cos 30^\circ }} \approx 2,3\)cm.
Bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số, bao gồm việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số trong các bài toán hình học.
Bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1, chúng tôi sẽ cung cấp lời giải chi tiết cho từng câu hỏi trong bài tập. Dưới đây là lời giải cho một số câu hỏi tiêu biểu:
Đề bài: Xác định hệ số góc của đường thẳng có phương trình 2x + 3y = 5.
Lời giải: Để xác định hệ số góc của đường thẳng có phương trình 2x + 3y = 5, ta cần đưa phương trình về dạng y = mx + c, trong đó m là hệ số góc. Ta có:
3y = -2x + 5
y = (-2/3)x + 5/3
Vậy, hệ số góc của đường thẳng là m = -2/3.
Đề bài: Viết phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc m = 3.
Lời giải: Phương trình đường thẳng có dạng y = mx + c. Thay tọa độ điểm A(1; 2) và hệ số góc m = 3 vào phương trình, ta có:
2 = 3 * 1 + c
c = 2 - 3 = -1
Vậy, phương trình đường thẳng là y = 3x - 1.
Để giải bài tập hàm số bậc nhất một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để học toán 9 hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 13 trang 85 sách bài tập toán 9 - Cánh diều tập 1. Chúc bạn học tập tốt và đạt kết quả cao trong môn toán!