Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 9. Bài viết này sẽ hướng dẫn bạn cách giải bài 60 trang 125 sách bài tập toán 9 - Cánh diều tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để giúp bạn hiểu rõ bản chất của bài toán.
Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng \(\frac{{5\pi R}}{6}\) a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH. b) Tính độ dài các cung AC, BC theo R. c) Kẻ OK vuông góc với AB tại K, tia OK cắt đường tròn (O) tại E. Tính diện tích hình quạt tròn EOB (giới hạn bởi cung nhỏ BE và hai bán kính OE, OB) theo R. d) Tính tỉ số phần trăm giữa diện tích hình quạt tròn BOC (giới hạn bởi cung nhỏ BC và hai bán
Đề bài
Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng \(\frac{{5\pi R}}{6}\)
a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH.
b) Tính độ dài các cung AC, BC theo R.
c) Kẻ OK vuông góc với AB tại K, tia OK cắt đường tròn (O) tại E. Tính diện tích hình quạt tròn EOB (giới hạn bởi cung nhỏ BE và hai bán kính OE, OB) theo R.
d) Tính tỉ số phần trăm giữa diện tích hình quạt tròn BOC (giới hạn bởi cung nhỏ
BC và hai bán kính OB, OC) và diện tích hình quạt tròn AOC (giới hạn bởi cung nhỏ AC và hai bán kính OA, OC).
Phương pháp giải - Xem chi tiết
a) Chứng minh tam giác AHC vuông cân, từ đó tính số đo cung CB.
b) Bước 1: Tính số đo cung nhỏ AB, AC.
Bước 2: Áp dụng công thức \(l = \frac{{\pi Rn}}{{180}}\).
c) Bước 1: Tính \(\widehat {BOE}\), từ đó suy ra số đo cung nhỏ EB.
Bước 2: Áp dụng công thức \(S = \frac{{\pi {R^2}n}}{{360}}\).
d) Tỉ số phần trăm = (diện tích quạt tròn BOC : Diện tích quạt tròn AOC).100%.
Lời giải chi tiết
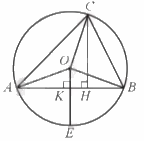
a) Ta có \(CH \bot AB\) nên \(\widehat {CHA} = 90^\circ \).
Xét tam giác AHC có \(\widehat {CHA} = 90^\circ \), \(HA = CH\) nên tam giác AHC vuông cân tại H, do đó \(\widehat {CAH} = 45^\circ \).
Mặt khác, góc CAH là góc nội tiếp chắn cung CB của (O) nên sđ\(\overset\frown{CB}=2\widehat{CAH}=2.45{}^\circ =90{}^\circ \).
Vậy điểm C nằm trên cung lớn AB sao cho số đo cung CB bằng 90⁰.
b) Độ dài cung nhỏ CB có số đo 90⁰ của (O; R) là \(\frac{{\pi R.90}}{{180}} = \frac{{\pi R}}{2}\).
Độ dài cung nhỏ AB có số đo n⁰ bằng \(\frac{{5\pi R}}{6}\) nên \(\frac{{\pi R.n}}{{180}} = \frac{{5\pi R}}{6}\), hay \(n = 150^\circ \), do đó số đo góc ở tâm \(\widehat {AOB} = 150^\circ \), suy ra sđ\(\overset\frown{AB}=150{}^\circ \).
Số đo cung nhỏ AC bằng \(360{}^\circ -\text{sđ}\overset\frown{CB}-\text{sđ}\overset\frown{AB}=360{}^\circ -90{}^\circ -150{}^\circ =120{}^\circ \).
Độ dài cung nhỏ AC là \(\frac{{\pi R.120}}{{180}} = \frac{{2\pi R}}{3}\).
c) Ta có \(OA = OB\left( { = R} \right)\) nên tam giác OAB cân tại O, mà \(OK \bot AB\) do đó OK là đường cao đồng thời là đường phân giác của tam giác OAB, suy ra \(\widehat {AOK} = \widehat {BOK} = \frac{{\widehat {AOB}}}{2} = \frac{{150^\circ }}{2} = 75^\circ \).
Góc BOK hay góc BOE là góc ở tâm chắn cung EB của (O) nên sđ \(\overset\frown{EB}=\widehat{BOE}=75{}^\circ \).
Diện tích quạt tròn EOB là \(\frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {R^2}.75}}{{360}} = \frac{{5\pi {R^2}}}{{24}}\).
a) Vì số đo cung CB bằng 90⁰ nên góc COB là góc ở tâm chắn cung CB cũng bằng 90⁰.
Diện tích quạt tròn BOC là \(\frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {R^2}.90}}{{360}} = \frac{{\pi {R^2}}}{4}\)
Diện tích quạt tròn AOC là \(\frac{{\pi {R^2}.120}}{{360}} = \frac{{\pi {R^2}}}{3}\)
Tỉ số phần trăm giữa diện tích quạt tròn BOC và Diện tích quạt tròn AOC là
\(\frac{{\pi {R^2}}}{4}:\frac{{\pi {R^2}}}{3}.100\% = 75\% \)
Bài 60 trang 125 sách bài tập toán 9 - Cánh diều tập 1 thuộc chương trình học toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế liên quan đến hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 60 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 60, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng, và giải thích cụ thể cho từng bước. Ví dụ:)
Ví dụ: Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Giải:
Hàm số y = 2x + 3 có dạng y = ax + b, trong đó:
Vậy, hệ số góc của hàm số là 2 và tung độ gốc là 3.
Ngoài việc giải chi tiết bài 60, chúng ta cũng cần nắm vững các dạng bài tập thường gặp và phương pháp giải để có thể tự tin giải quyết các bài tập tương tự. Dưới đây là một số dạng bài tập thường gặp:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, bạn cần lưu ý những điều sau:
Bài 60 trang 125 sách bài tập toán 9 - Cánh diều tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc nhất. Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!